In this exercise, we will create a class that represents a vector in 3D space. Such a class would be crucial in applications such as a 3D game-engine.

In previous exercises, we have considered the representation of vectors in a 2D space. We now extend this to 3D space. We previously specified the points in Cartesian coordinates, and wrote static methods for converting them into polar coordinates. In the exercise, we will do the same, except that we will extend our Cartesian coordinates from \( (x,y) \) to \( (x, y, z) \), and instead of using polar coordinates \( (r, \theta) \), we will use spherical coordinates \( (r, \theta, \phi) \). Given a point in 3D space specified by such coordinates, \( r \) is the radial distance of that point from a fixed origin, \( \theta \) is its inclination angle measured from a fixed zenith direction, and \( \phi \) is the azimuth angle of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith.

Here’s a useful illustration from Wikipedia:

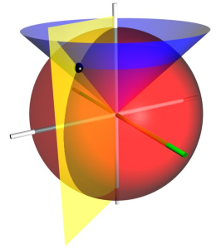
Illustration of spherical coordinates. The red sphere shows the points with \( r = 2 \), the blue cone shows the points with inclination (or elevation) \( \theta = 45\deg \), and the yellow half-plane shows the points with azimuth \( \phi = -60\deg \). The zenith direction is vertical, and the zero-azimuth axis is highlighted in green. The spherical coordinates \( (2, 45\deg, -60\deg) \) determine the point of space where those three surfaces intersect, shown as a black sphere.

For more information, see the Wikipedia entry on Spherical Coordinates.

We will use the following definitions for converting between coordinate systems:

and conversely:

Here is the API for the class Vector3D:

public Vector3D(double x, double y, double z)

Class constructor

public double getR()

Return the radial distance \( r \).

public double getTheta()

Return the inclination \( \theta \).

public double getPhi()

Return the azimuth \( \phi \).

public static Vector3D add(Vector3D lhs, Vector3D rhs)

Return the sum of two 3D vectors.

public static Vector3D subtract(Vector3D lhs, Vector3D rhs)

Return the difference of two 3D vectors.

public static Vector3D scale( Vector3D v, double scaleFactor)

Return the result of scaling v by scalefactor.

Write a Vector3D class which meets this API.

Hint: for Vector3D.getTheta() there are two arctan methods available in the java.lang.Math class - make sure you choose the appropriate one.