In this question, we will write a program that converts from Cartesian coordinates to polar coordinates.

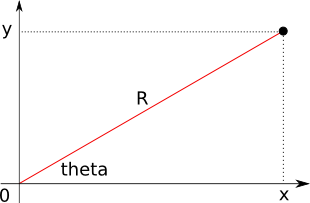
You are probably used to dealing with Cartesian or (x, y) coordinates, to specify points on a graph for example. However, another way that we can define the location of points on a 2D plane is to specify a distance from the origin, and an angle from the x-axis.

The distance from the origin is typically termed \( R \), and the angle from the x-axis is typically called \( \theta \) .

It is useful to be able to convert between the two coordinates; in this exercise, we will write a program to convert from (x, y) to (\( R \), \( \theta \) ).

From the figure, we can see that:

• \( y = R \sin \theta \)
• \( x = R \cos \theta \)

so we can divide one equation by another to get:

and since \( \sin^2 \theta + \cos^2 \theta = 1 \), with some rearranging:

• \( y^2 = R^2 \sin^2 \theta \)
• \( x^2 = R^2 \cos^2 \theta \)

so

• \( x^2 + y^2 = R^2 \cos^2 \theta + R^2 \sin^2 \theta = R^2 ( \cos^2 \theta + \sin^2 \theta ) = R^2 \)
• \( R = \sqrt{x^2 + y^2} \)

Create a program, using a class called PolarCoordinates, and as before create a main() method. Your program will read two arguments of type double from the command line, and these are to be interpreted as the Cartesian coordinates (x, y). Your program should return these points in polar coordinates \( R \) and \( \theta \). For example:

: java PolarCoordinates 1.0 0.0
1.0
0.0

: java PolarCoordinates -2.0 0.0
2.0
3.14159

: java PolarCoordinates  0.0 3.0
3.0
1.5707