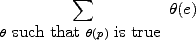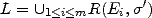PDDL
-- The Planning Domain
Definition Language
Version 1.2
| This manual was produced by the AIPS-98
Planning Competition Committee: |
| |
Malik Ghallab, Ecole Nationale Superieure
D’ingenieur des |
|
Constructions
Aeronautiques |
|
Adele Howe (Colorado State
University) |
|
Drew McDermott (chair) (Yale
University) |
|
Ashwin Ram (Georgia Tech
University) |
|
Manuela Veloso (Carnegie Mellon
University) |
|
Daniel Weld (University of
Washington) |
| It was based on the UCPOP language manual,
written by the following |
| researchers from the University of
Washington: |
| |
Anthony Barrett, Dave Christianson, Marc
Friedman, Chung Kwok, |
|
Keith Golden, Scott Penberthy, David E Smith,
Ying Sun, |
| Contact Drew McDermott
(drew.mcdermott@yale.edu) with comments. |
Yale Center for Computational Vision and
Control
Tech Report CVC TR-98-003/DCS TR-1165
October, 1998
Abstract
This manual describes the syntax of
PDDL, the Planning
Domain Definition Language, the problem-specification
language for the AIPS-98 planning competition. The language
has roughly the the expressiveness of Pednault’s
ADL [?] for propositions, and
roughly the expressiveness of UMCP [?] for
actions. Our hope is to encourage empirical evaluation of
planner performance, and development of standard sets of
problems all in comparable notations.
1 Introduction
This manual describes the syntax, and, less
formally, the semantics, of the Planning Domain Definition Language
(PDDL). The language supports
the following syntactic features:
- Basic STRIPS-style actions
- Conditional effects
- Universal quantification over dynamic universes
(i.e., object creation and
destruction),
- Domain axioms over stratified theories,
- Specification of safety constraints.
- Specification of hierarchical actions composed
of subactions and subgoals.
- Management of multiple problems in multiple
domains using differing subsets of language features (to support
sharing of domains across different planners that handle varying
levels of expressiveness).
PDDL is
intended to express the “physics” of a domain, that is,
what predicates there are, what actions are possible, what the
structure of compound actions is, and what the effects of actions
are. Most planners require in addition some kind of
“advice,” that is, annotations about which actions to
use in attaining which goals, or in carrying out which compound
actions, under which circumstances. We have endeavored to provide
no advice at all as part of the PDDL notation; that explains the almost
perverse aura of neutrality surrounding the notation at various
places. As a result of this neutrality, almost all planners will
require extending the notation, but every planner will want to
extend it in different ways.
Even with advice left out, we anticipate that few
planners will handle the entire PDDL language. Hence we have factored the
language into subsets of features, called requirements. Every domain defined using
PDDL should declare which
requirements it assumes. A planner that does not handle a given
requirement can then skip over all definitions connected with a
domain that declares that requirement, and won’t even have to
cope with its syntax.
PDDL is
descended from several forebears:
- ADL [?]
- The SIPE-2 formalism [?]
- The Prodigy-4.0
formalism [?]
- The UMCP formalism [?]
- The Unpop formalism [?]
- and, most directly, the UCPOP
formalism [?]
Our hope is to encourage sharing of problems and
algorithms, as well as to allow meaningful comparison of the
performance of planners on different problems. A particular goal is
to provide a notation for problems to be used in the AIPS-98
planning contest.
2 A Simple Example
To give a flavor of the language, consider
Pednault’s famous example [?]
involving transportation of objects between home and work
using a briefcase whose effects involve both universal
quantification (all
objects are moved) and conditional effects (if they are inside the briefcase when
it is moved). The domain is described in terms of three
action schemata (shown below). We encapsulate these schemata
by defining the domain and listing its requirements.
|
(define (domain briefcase-world)
(:requirements :strips :equality :typing :conditional-effects)
(:types location physob)
(:constants (B - physob))
(:predicates (at ?x - physob ?l - location)
(in ?x ?y - physob))
... |
A domain’s set of requirements allow a
planner to quickly tell if it is likely to be able to handle the
domain. For example, this version of the briefcase world requires
conditional effects, so a straight STRIPS-representation planner
would not be able to handle it. A keyword (symbol starting with a
colon) used in a :requirements
field is called a requirement
flag; the domain is said to declare a requirement for that flag.
All domains include a few built-in types, such as
object (any object), and
number. Most domains define
further types, such as location
and physob (“physical
object”) in this domain.
A constant is a symbol that will have the same
meaning in all problems in this domain. In this case
B -- the briefcase -- is
such a constant. (Although we could have a type briefcase, we don’t need it,
because there’s only one briefcase.)
Inside the scope of a domain declaration, one
specifies the action schemata for the domain.
|
(:action mov-b
:parameters (?m ?l - location)
:precondition (and (at B ?m) (not (= ?m ?l)))
:effect (and (at b ?l) (not (at B ?m))
(forall (?z)
(when (and (in ?z) (not (= ?z B)))
(and (at ?z ?l) (not (at ?z ?m)))))) ) |
This specifies that the briefcase can be moved
from location ?m to location
?l, where the symbols starting
with question marks denote variables. The preconditions dictate
that the briefcase must initially be in the starting location for
the action to be legal and that it is illegal to try to move the
briefcase to the place where it is initially. The effect equation
says that the briefcase moves to its destination, is no longer
where it started, and everything inside the briefcase is likewise
moved.
|
(:action put-in
:parameters (?x - physob ?l - location)
:precondition (not (= ?x B))
:effect (when (and (at ?x ?l) (at B ?l))
(in ?x)) ) |
This action definition specifies the effect of
putting something (not the briefcase (B) itself!) inside the briefcase. If the
action is attempted when the object is not at the same place
(?l) as the briefcase, then
there is no effect.
|
(:action take-out)
:parameters (?x - physob)
:precondition (not (= ?x B))
:effect (not (in ?x)) ) |
The final action provides a way to remove
something from the briefcase.
Pednault’s example problem supposed that at
home one had a dictionary and a briefcase with a paycheck inside
it. Furthermore, suppose that we wished to have the dictionary and
briefcase at work, but wanted to keep the paycheck at home. We can
specify the planning problem as follows:
|
(define (problem get-paid)
(:domain briefcase-world)
(:init (place home) (place office)
(object p) (object d) (object b)
(at B home) (at P home) (at D home) (in P))
(:goal (and (at B office) (at D office) (at P home)))) |
One could then invoke a planner by typing
something like (graph-plan
'get-paid). The planner checks to see if it can handle the
domain requirements and if so, plans.
3 Syntactic Notation
Our notation is an Extended BNF (EBNF) with the
following conventions:
As we said in Section 1
, PDDL is intended to express only the
physics of a domain, and will require extension to represent the
search-control advice that most planners need. We recommend that
all such extensions obey the following convention: An extended
PDDL expression is an ordinary
PDDL expression with some
subexpressions of the form (
 e
a), where
e is an unextended
PDDL expression and
a is some advice. The
“
e
a), where
e is an unextended
PDDL expression and
a is some advice. The
“
 ” notation indicates
that we are ascending to a “meta” level. The word
“expression” here is interpreted as “any
part of a PDDL expression
that is either a single symbol or an expression of the form
(...).” For
instance, the definition of mov-b given above might be enhanced
for a particular planner thus:
” notation indicates
that we are ascending to a “meta” level. The word
“expression” here is interpreted as “any
part of a PDDL expression
that is either a single symbol or an expression of the form
(...).” For
instance, the definition of mov-b given above might be enhanced
for a particular planner thus:
|
(:action mov-b
:parameters (?m ?l - location)
:precondition (and (^^ (at B ?m)
(goal-type: achievable))
(^^ (not (= ?m ?l))
(goal-type: filter)))
:effect (and (at b ?l) (not (at B ?m))
(forall (?z)
(when (and (in ?z) (not (= ?z B)))
(and (^^ (at ?z ?l) :primary-effect)
(^^ (not (at ?z ?m)) :side-effect)))))) |
to indicate that
- (:primary-effect
vs. :side-effect): when
the planner encounters a goal of the form (at ?z ?l), it may introduce a
mov-b action into a plan
in order to achieve that goal, but a goal of the form
(not (at ?z ?m)), while
it may be achieved by an action of this form introduced for
another reason, should not cause a mov-b action to be created;
- (different
goal-types): If an action such
as (mov-b b1 place2 place2)
arises, it should be rejected immediately, rather than giving rise
to a subgoal (not (= place2
place2)).
Adopting this convention should improve the
portability of plan-problem collections, because a planner using
PDDL can be written to ignore
all advice in unexpected contexts. In the future, we may introduce
a more complex syntax for attaching advice to be used by different
planners, but for now the only general principle is that an
expression of the form (
 e
a) can occur
anywhere, and will mean exactly the same thing as
e, as far as domain
physics are concerned.
e
a) can occur
anywhere, and will mean exactly the same thing as
e, as far as domain
physics are concerned.
Comments in PDDL begin with a semicolon
(“;”) and end with
the next newline. Any such string behaves like a single space.
4 Domains
We now describe the language more formally. The
EBNF for defining a domain structure is:
| |
<domain> |
::= (def |
ine (domain <name>) |
|
[<domain-vars-def>]:expression-
evaluation |
|
[<safety-def>]:safety-
constraints |
|
<extension-def> |
::= (:extends <domain name>+) |
|
<require-def> |
::= (:requirements <require-key>+) |
|
<require-key> |
::= See
Section 15
|
|
<types-def> |
::= (:types <typed list (name)>) |
|
<constants-def> |
::= (:constants <typed list (name)>) |
|
<domain-vars-def> |
::= (:dom |
ain-variables |
|
|
|
<typed
list(domain-var-declaration)>) |
|
<predicates-def> |
::= (:predicates <atomic formula
skeleton>+) |
|
<atomic
formula skeleton> |
|
|
::= (<predicate> <typed list
(variable)>) |
|
<timeless-def> |
::= (:timeless <literal (name)>+) |
|
<structure-def> |
::= <action-def> |
|
<structure-def> |
::=:domain
-axioms <axiom-def> |
|
<structure-def> |
::=:action
-expansions <method-def> |
Although we have indicated the arguments in a particular order,
they may come in any order, except for the (domain ...) itself.
Proviso: For
the convenience of some implementers, we define a “strict
subset” of PDDL that
imposes the following additional restrictions:
- All keyword
arguments (for (define (domain
...)) and all similar constructs) must appear in the order
specified in the manual. (An argument may be omitted.)
- Just one
PDDL definition (of a domain,
problem, etc.) may appear per file.
- Addenda (see
Section 11
) are forbidden.
Names of domains, like other occurrences of
syntactic category <name>, are strings of characters beginning
with a letter and containing letters, digits, hyphens
(“-”),and underscores (“_”). Case is not
significant.
If the :extends argument is present, then this
domain inherits requirements, types, constants, actions, axioms,
and timelessly true propositions from the named domains, which are
called the ancestors of this
domain.
The :requirements field is intended to
formalize the fact that not all planners can handle all problems
statable in the PDDL notation.
If the requirement is missing (and not inherited from any ancestor
domain), then it defaults to :strips. In general, a domain is taken to
declare every requirement that any ancestor declares. A description
of all possible requirements is found in Section 15.
The :types
argument uses a syntax borrowed from Nisp [?] that is used
elsewhere in PDDL (but only if
:typing is handled by the
planner.
|
<typed list (x)> |
::=:typing
x+- <type> <typed list(x)> |
|
<type> |
::= (either <type>+) |
|
<type> |
::=:fluents (fluent
<type>) |
A typed list is used to declare the types of a list of entities;
the types are preceded by a minus sign (“-”), and every other element of the
list is declared to be of the first type that follows it, or
object if there are no types
that follow it. An example of a <typed
list(name)> is
integer float -
number physob
If this occurs as a :types argument to a domain, it declares
three new types, integer,
float, and physob. The first two are subclasses of
number, the last a subclass of
object (by default). That is,
every integer is a number, every float is a number, and every
physical object is an object.
An atomic type name is just a timeless unary
predicate, and may be used wherever such a predicate makes sense.
In addition to atomic type names, there are two compound types.
(either t1
...tk) is the
union of types t1 to
tk. (fluent t) is
the type of an object whose value varies from situation to
situation, and is always of type t. (See Section 12.)
The :domain-variables declaration is used for
domains that declare the requirement flag :expression-evaluation; this requirement,
and the accompanying syntactic class domain-var-declaration, are described in
Section 12
.
The :constants field has the same syntax as the
:types field, but the semantics
is different. Now the names are taken as new constants in this
domain, whose types are given as described above. E.g., the
declaration
| (:constants |
sahara - theater |
|
division1 division2 -
division) |
indicates that in this domain there are three
distinguished constants, sahara
denoting a theater and two
symbols denoting divisions.
The :predicates field consists of a list of
declarations of predicates, once again using the typed-list syntax
to declare the arguments of each one.
The :timeless
field consists of a list of literals that are taken to be true at
all times in this domain. The syntax <literal(name)> will be defined in
Section 6. It
goes without saying that the predicates used in the timeless
propositions must be declared either here or in an ancestor domain.
(Built-in predicates such as “=” behave as if they were inherited
from an ancestor domain, although whether they actually are
implemented this way depends on the implementation.)
The remaining fields define actions and rules in
the domain, and will be given their own sections.
5 Actions
The EBNF for an action definition is:
| |
<action-def> |
::= (:act |
ion <action functor> |
|
:parameters ( <typed list (variable)> ) |
|
<action functor> |
::= <name> |
|
<action-def body> |
::= |
[:vars (<typed list(variable)>)]
| :existential-preconditions |
| :conditional-effects | |
|
<action
spec>]:action-
expansions |
|
[:expansion :methods]:action-
expansions |
|
[:maintain <GD>]:action-
expansions |
|
[:only-in-expansions <boolean>]:action-
expansions |
The :parameters list is simply
the list of variables on which the particular rule operates,
i.e., its arguments, using the
typing syntax described above. The :vars list are locally bound variables
whose semantics are explained below.
The :precondition is an optional goal
description (GD) that must be satisfied before the action is
applied. As defined below (Section 6
), PDDL goal descriptions are quite
expressive: an arbitrary function-free first-order logical sentence
is allowed. If no preconditions are specified, then the action is
always executable. Effects list
the changes which the action imposes on the current state of the
world. Effects may be universally quantified and conditional, but
full first order sentences (e.g., disjunction and Skolem functions) are
not allowed. Thus, it is important to realize that
PDDL is asymmetric:
action preconditions are considerably more expressive than
action effects.
The :effect
describes the effects of the action. See Section 7.
If the domain declares requirement
:action-expansions, then
it is legitimate to include an :expansion field for an action, which
specifies all the ways the action may be carried out in terms
of (presumably simpler) actions. It is also meaningful to
impose a constraint that a <GD> be maintained throughout the
execution of an action. See Section 8 .
An action definition must have an
:effect or an
:expansion, but
not both.
Free variables are not allowed. All variables in
an action definition (i.e., in
its preconditions, maintenance condition, expansion, or effects)
must be included in the :parameter or :vars list, or explicitly introduced with a
quantifier.
:vars is
mainly a convenience. Variables appearing here behave as if bound
existentially in preconditions and universally in effects, except
that it is an error if more than one instance satisfies the
existential precondition. So, for example, in the following
definition
|
(:action spray-paint
:parameters (?c - color)
:vars (?x - location)
:precondition (at robot ?x)
:effect (forall (?y - physob)
(when (at ?y ?x)
(color ?y ?c)))) |
if the robot must be in at most one place to avoid an error.
All the variables occurring free in the
:effect or :action field must be bound in the
:precondition field.
The optional argument :only-in-expansions is described in
Section 8
.
6 Goal Descriptions
A goal description is used to specify the
desired goals in a planning problem and also the preconditions for
an action. Function-free first-order predicate logic (including
nested quantifiers) is allowed.
| |
<GD> |
::= <atomic formula(term)> |
|
<GD> |
::=:disjunctive
-preconditions (or
<GD>*) |
|
<GD> |
::=:disjunctive
-preconditions (not
<GD>) |
|
<GD> |
::=:disjunctive
-preconditions (imply
<GD> <GD>) |
|
<GD> |
::= |
:existential-preconditions |
|
(exists (<typed list(variable)>*)
<GD> ) |
|
<GD> |
::= |
:universal-preconditions |
|
(forall (<typed list(variable)>*)
<GD> ) |
|
<literal(t)> |
::= <atomic formula(t)> |
|
<literal(t)> |
::= (not <atomic formula(t)>) |
|
<atomic formula(t)> |
::= (<predicate> t*) |
where, of course, an occurrence of a
<predicate> should agree with its declaration in
terms of number and, when applicable, types of arguments.
Hopefully the semantics of these expressions is
obvious.
7 Effects
PDDL allows both conditional and
universally quantified effects. The description is
straightforward:
| |
<effect> |
::= (and <effect>*) |
|
<effect> |
::= (not <atomic formula(term)>) |
|
<effect> |
::= <atomic formula(term)> |
|
<effect> |
::=:conditional
-effects (forall
(<variable>*)
<effect>) |
|
<effect> |
::=:conditional
-effects (when
<GD> <effect>) |
|
<effect> |
::=:fluents(change
<fluent> <expression>) |
We assume that all variables must be bound (either with a
quantifier or in the parameters section of an action definition).
As in S
TRIPS,
the truth value of predicates are assumed to persist forward in
time. Unlike STRIPS,
PDDL has no delete list
-- instead of deleting (on a b)
one simply asserts (not (on a
b)). If an action’s
effects does not mention a predicate P then the truth of that predicate is
assumed unchanged by an instance of the action.
The semantics of (when P
E) are as follows: If
P is true before the action,
then effect E occurs after.
P is a secondary
precondition [?]. The action is feasible
even if P is false, but
the effect E occurs only
if P is true.
Fluents are explained in Section 12.
8 Action Expansions
In many classical hierarchical planners (such as
Sipe [?], O-Plan [?], and
UMCP [?]) goals are specified in terms of
abstract actions to carry out as well as (or instead of) goals to
achieve. A solution to a planning problems is a sequence of actions
that jointly compose all the abstract actions originally requested.
PDDL allows for this style of
planning by providing an :expansion field in action definitions,
provided the domain declares requirement :action-expansions. The field, as described
above, is of the form :expansion <action
spec>, where
<action spec> has the following syntax:
| |
<action spec> |
::= <action-term> |
|
<action spec> |
::= (in- |
context <action spec> |
|
<action spec> |
::= (choice <action spec>*) |
|
<action spec> |
::= (for |
some (<typed list(variable)>*) |
|
<action spec> |
::= (series <action spec>*) |
|
<action spec> |
::= (parallel <action spec>*) |
|
<action spec> |
::= (tag |
<action-label term>* |
|
<action spec> |
::= |
:foreach-expansions |
|
(foreach |
<typed
list(variable)> |
|
<action spec> |
::= |
:dag-expansions |
|
(con |
strained (<action spec>+) |
|
<action constraint> |
::= (in- |
context <action constraint> |
|
<action constraint> |
::= (series <action constraint>*) |
|
<action constraint> |
::= (parallel <action constraint>*) |
|
<action-term> |
::= (<action functor> <term>*) |
|
<action-label term> |
::= |
<action
label> |
|
<action label> |
::= <name> |
Extra choices may be added to an action expansion after the action
is defined, by the use of :methods, as described in
Section 11
. An action with no expansion is
called a primitive action, or
just a primitive. It is always
possible to tell by the action definition if the action is
primitive; if all its expansions are defined via methods, then the
:expansion argument should be
the symbol :methods.
An action may be expanded into a structure of
actions, either a series-parallel combination, or, if the domain
declares requirement :dag-expansions an arbitrary partial order
(with steps labeled by tag). If
there is a choice of expansions, it is indicated using
choice. A forsome behaves like a choice among
all its instances.
The only built-in action term is
(--), or no-op.
Anywhere an action is allowed, the expansion may
have an expression of the form
|
(in-c |
ontext <action
spec> |
This construct is used to declare preconditions
and maintenance conditions of actions that are due purely to their
occurring in the context of this expansion. (It should
not be used to repeat the
preconditions associated with the definition of the action
itself.) For example, to indicate a plan to evacuate an area
of friendly forces and then shell it, one might write
|
(series (clear ?area)
(in-context (shell ?area)
:precondition (not (exists (?x - unit)
(and (friendly ?x) (in ?x ?area)))))) |
As syntactic sugar, PDDL allows you to write
(achieve P) as an abbreviation for (in-context (--) :precondition
P).
The (constrained A
C*) syntax allows fairly arbitrary further
conditions to be imposed on an action spec, with labels standing in
for actions and their endpoints. The labels are defined by the
(tag labels action) construct. A label stands for the whole
action (occurrence) unless it is qualified by < or >, in which case it stands for the
beginning or end of the action. Inside C, (series l1
l2 ...lk)
imposes an additional ordering requirement on the time points
tagged l1,...,lk.
(in-context (series
l1 ...lk)
-conditions-) can be used to impose extra
conditions (or announce extra effects) of the interval
corresponding to such an additional ordering.
For example, to expand an action into four
subactions (A),
(B), (C), and (D), such that (A) precedes (B) and (D), and (C) precedes (D), with condition (P) maintained from the end of
(A) until the end of
(D), write
|
:expansion (constrained ((series (tag A (> end-a)) (B))
(series (C) (tag (< beg-d) (D) (> end-d))))
(in-context (series end-a beg-d end-d)
:maintain (P))) |
As an illustration of all this, here is a
fragment of the University of Maryland Translog
domain [?], specifying how to unload a
flatbed truck:
|
(:action unload
:parameters (?p - package ?v - vehicle ?l - location)
:expansion
(choice
... ; several choices elided
(forsome (?c - crane)
(in-context
(constrained
(series (tag (pick-up-package-vehicle
?p ?c ?v ?l)
(> end-n1))
(tag (< beg-n2)
(put-down-package-ground
?p ?c ?l)))
(in-context (series end-n1 beg-n2)
:maintain (and (at-package ?p ?c)
(at-equipment ?c ?l))))
:precondition (and (flatbed ?v)
(empty ?c)
(at-package ?p ?v)
(at-vehicle ?v ?l)
(at-equipment ?c ?l))))))
|
Note that PDDL does not allow
you to specify whether it makes
sense to insert steps to achieve an in-context precondition
of a choice (as opposed to using it as a “filter”
condition). That falls into the category of advice, which is
handled in a planner-specific way.
The parallel
construct imposes no constraints on the execution order of its
arguments. However, a label associated with a parallel composition
is associated with the first action of the composition to begin, in
the case of a “<” label, or the last action to
end, in the case of a “>.” E.g., to indicate that a
condition be true from the end of act1 until a set of actions performed in
parallel with act1 are
finished, write
|
(constrained (tag (parallel (tag (act1) (> end-act1))
(act2)
...
(actN))
(> alldone))
(in-context (series end-act1 alldone)
:maintain (condition))) |
If the domain declares requirement
:foreach-expansions, then
an action can have an expansion of the form (foreach (v) P(v) A(v)), where v is a set of typed variables,
P(v) is a precondition, and
A(v) is an action spec. The idea is to
expand the action into zero or more occurrences of
A(v), one for each instance of
P(v) that is true before in the
situation when the expanded action begins execution. (See
Appendix A
for a precise definition of
what it means for an action-spec to be satisfied by an action
sequence.)
The syntax of the language permits labels to
occur inside choice and
foreach action specs. It is a
consequence of the formal semantics of Appendix A that (a) a constraint
mentioning a label inside a choice branch that doesn’t occur
doesn’t constrain anything; (b) a constraint mentioning a
reference to a label inside a foreach or forsome from outside doesn’t
constrain anything.
In Section 5
we mentioned that an action
definition may contain an argument
If this is t
(default is nil), then a
planner is not allowed to assume that instances of the action are
feasible if its preconditions are satisfied. Instead, it can
include an action in a plan only if it occurs as the expansion of
some other action. The intended use of this notation is to indicate
that we do not really know all the preconditions of the action,
just some standard contexts in which the preconditions are sure to
be satisfied.
See Section 11
for a notation that allows
cumbersome action expansions to be broken into more manageable
pieces.
9 Axioms
Axioms are logical formulas that assert
relationships among propositions that hold within a situation (as
opposed to action definitions, which define relationships across
successive situations). To have axioms, a domain must declare
requirement :domain-axioms.
| |
<axiom-def> |
::= (:axi |
om <GD>) |
|
:vars (<typed list (variable)>) |
|
:implies <literal(term)>) |
The :vars
field behaves like a universal quantifier. All the variables that
occur in the axiom must be declared here.
For example, we might define the classical
blocks-world predicates above
and clear as follows:
|
(:axiom
:vars (?x ?y - physob)
:context (on ?x ?y)
:implies (above ?x ?y)))
(:axiom
:vars (?x ?y - physob)
:context (exists (?z - physob)
(and (on ?x ?z) (above ?z ?y)))
:implies (above ?x ?y))
(:axiom
:vars (?x - physob)
:context (or (= ?x Table)
(not (exists (?b - block)
(on ?b ?x))))
:implies (clear ?x)) |
Unless a domain declares requirement
:true-negation,
not is treated using the
technique of “negation as failure” [?]. That
means it makes no sense to conclude a negated formula; they
should occur only as deductive goals, when (not g) succeeds if and only if
g fails. (If g contains variables, the results are
undefined.) Hence axioms are treated directionally, always
used to conclude the :implies field, and never to conclude
a formula from the :context field. (Of course, whether
an axiom is used forward or backward is a matter of advice,
and PDDL is silent on
this issue.)
Another important reason for the directionality
of axioms is to avoid overly complex interactions with action
definitions. The rule is that action definitions are not allowed to
have effects that mention predicates that occur in the
:implies field of an
axiom. The intention is that action definitions mention
“primitive” predicates like on, and that all changes in truth
value of “derived” predicates like above occur through axioms. Without
axioms, the action definitions will have to describe changes
in all predicates that might be affected by an action, which
leads to a complex software engineering (or “domain
engineering”) problem.
If a domain declares requirement
:true-negation (which
implies :open-world),
then exactly how action definitions interact with axioms
becomes hard to understand, and the management takes no
responsibility for the outcome. (For example, if there is an
axiom P  Q
Q
 R, and an action causes (not R) when P and Q are true, does P become false or Q?)
R, and an action causes (not R) when P and Q are true, does P become false or Q?)
The domain requirement :subgoal-through-axioms indicates that a
goal involving derived predicates may have to be solved by finding
actions to change truth values of related primitive predicates. For
example, a goal (above A B)
might be achieve by either achieving (on A B) or achieving (and (an A Z)
(above Z
B)) for some Z. A domain that does not declare
this requirement may still have axioms, but they will be used
only for timeless predicates.
Note that a given predicate can be in the
:implies field of more than one
axiom.
10 Safety Constraints
A domain declaring requirement
:safety-constraints is
allowed to specify safety
constraints, defined as background goals that must be
satisfied throughout the planning process. A plan is allowed
only if at its end none of these background goals is false.
In other words, if one of the constraints is violated at some
point in the plan, it must become true again by the end.
|
<safety-def> ::= (:safety <GD>) |
For example, one could command a softbot
(software robot) to avoid deleting files that are not backed up on
tape with the following constraint:
|
(:safety
(forall (?f)
(or (file ?f) (written-to-tape ?f)))) |
As everywhere else in PDDL, free variables are not allowed.
It is important to note that safety constraints
do not require an agent to
make them true; rather, the
agent must avoid creating new
violations of the constraints. For example, if a constraint
specifies that all of my files be read protected, then the agent
would avoid changing any of my files to be readable; but if my
.plan file is already readable
in the initial state, then the agent would not protect that file.
For details of safety constraints, please refer
to [?].
Safety constraints should not be confused with
:timeless propositions. (See
Section 4.)
Timeless propositions are always true in all problems in the
domain, and it should be impossible for any action to change them.
Hence no special measures are required to ensure that they are not
violated.
11 Adding Axioms and Action Expansions Modularly
Although PDDL allows a domain to be defined as one
gigantic define, it is often
more convenient to break the definition into pieces. The following
notation allows adding axioms and action expansions to an existing
domain:
| |
(def |
ine (addendum <name>) |
|
<extra-def> |
::= <action-def> |
|
<extra-def> |
::=:domain
-axioms <axiom-def> |
|
<extra-def> |
::=:action
-expansions <method-def> |
|
<extra-def> |
::=:safety
-constraints <safety-def> |
|
<method-def> |
::= (:met |
hod <action functor> |
|
:parameters ( <typed list (variable)> ) |
Please remember that, as explained in
Section 4,
in the “strict subset” of PDDL addenda are not allowed.
Inside a (define
(addendum ...) ...) expression, :actions and :axioms behave as though they had been
included in the original (define
(domain ...) ...) expression for the domain.
:method declarations
specify further choice points for the expansion of an
already-declared action, almost as though the given
<action-def body> included inside a choice in the original expansion of
the action. (It doesn’t work quite that neatly because
the parameters may have new names, and because an
<action-def body> is not exactly what’s
expected in a choice.)
In a method definition, the <action-def
body> may not have an
:effect field or an
:only-in-expansions
field.
Method names are an aid in describing problem
solutions as structures of instantiated action schemas. Each action
has its own space of method names; there is no need to make them
unique over a domain. If an action has a method supplied in its
original definition, the name of that method is the same as the
name of the action itself.
Example:
|
(define (addendum carry-methods)
:domain translog
...
(:method CARRY-VIA-HUB
:name usual
:parameters (?p - package ?tc ?tc - tcenter)
:expansion (forsome (?hub - hub)
(in-context (series (carry-direct ?p ?tc1 ?hub)
(carry-direct ?p ?hub ?tc2))
:precondition (exists (?city1 ?city2 - city
?reg1 ?reg2 - region)
(and (in-city ?tc1 ?city1)
(in-city ?tc2 ?city2)
(in-region ?city1 ?reg1)
(in-region ?city2 ?reg2)
(serves ?hub ?reg1)
(serves ?hub ?reg2)
(available ?hub)))))
:precondition (not (hazardous ?p)))
...) |
The reason to give addenda names is so the system
will know when an addendum is being redefined instead of being
added for the first time. When a (define (addendum N) ...)
expression is evaluated, all the material previously associated
with N is erased before the
definitions are added. The name of an addendum is local to its
domain, so different domains can have addenda with the same name.
12 Expression Evaluation
If a domain declares requirement
:expression-evaluation,
then it supports a built-in predicate (eval E
V ) that succeeds
if the value of expression E is V . E has Lisp-like syntax for
expressions, which should at least allow functions
+, -, *, and /; this argument position is said to
be an evaluation context.
Evaluation contexts are the only places in PDDL where functions are allowed,
except for terms denoting actions. E should not include any variables;
if it does, the goal will fail in an implementation-dependent
way. (Some implementations will distinguish between failure
due to E’s value
being different from V
and failure due to the inability to generate all instances of
E. Cf. equation, below.)
Another evaluation context is the argument to
(test E).
Here E is an expression whose
main functor is one of =,
>, <, >=,
or <=. The expression is evaluated, and the
goal succeeds if it evaluates to T.
The goal (bounded-int I
L H) succeeds if
I is an integer in the interval
[L,H]. L and H
are evaluation contexts.
The goal (equation L
R) tries to bind
variables so that L and
R are equal. Both
L and R are evaluation contexts, but if
there is an unbound variable, it is bound to whatever value
would make L and
R evaluate to the same
thing. E.g., if ?y has
been bound to 6, and ?x
is unbound, then (equation (+ ?x
2) (- ?y 3)) will bind ?x to 1. Don’t expect an
implementation to do anything fancy here; every
implementation should at least handle the case where there is
a single occurrence of an unbound variable, buried at most
inside an expression of the form (+ ...).
The domain-vars defined in (define (domain...) ...) expressions are
evaluated in evaluation contexts. The syntax is
| |
<domain-vars-def> |
::= (:dom |
ain-variables |
|
<typed
list(domain-var-declaration)> |
|
<domain-var-declaration
> |
::= <name> -- (<name>
<constant>) |
E.g.:
|
(define (domain cat-in-the-hat)
(:types thing)
(:domain-variables (numthings 2) - integer)
...
(:axiom
:vars (?i - integer)
:context (bounded-int ?i 1 numthings)
:implies (thing ?i))) |
A variable like this is scoped over the entire
domain, and is inherited by domains that extend this one. If the
variable is redeclared in an extending theory, it shadows the
original binding.
If a domain declares requirement
:fluents, then it
supports the type (fluent
<type>), plus some new predicates. A fluent
is a term with time-varying value (i.e., a value that can
change as a result of performing an action). The proposition
(current-value
F V ) is true in a situation if
V is the current value of
F in that situation.
Further, if a planner handles the :fluents requirement, then there must
be a built-in predicate (fluent-eval E V ), which succeeds if V is the value of E, using the current value of any
fluent that occurs in E
(and otherwise behaving like eval). Similarly, there is a
predicate fluent-test
that is to test as
fluent-eval is to
eval. In addition, there
is an effect (change
F E) that changes the value of fluent
F to E. E is an evaluation context, and its
value is computed with respect to the situation obtaining
before the action (cf. when).
|
(:action pour
:parameters (?source ?dest - container)
:vars (?sfl ?dfl - (fluent number) ?dcap - number)
:precondition (and (contents ?source ?sfl)
(contents ?dest ?dfl)
(capacity ?dest ?dcap)
(fluent-test (<= (+ ?sfl ?dfl) ?dcap)))
:effect (when (and (contents ?source ?sfl)
(contents ?dest ?dfl))
(and (change ?sfl 0)
(change ?dfl (+ ?dfl ?sfl))))) |
One of the additional built-in functions that
comes with requirement :fluents
is (sum v p e).
This is a fluent whose value in a situation is
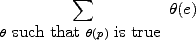 v declares all the variables of
p that aren’t already
bound. e is a fluent-evaluation
context. For example,
v declares all the variables of
p that aren’t already
bound. e is a fluent-evaluation
context. For example,
|
(fluent-eval (sum (?p - person ?w - number)
(and (aboard ?p ?elevator)
(weight ?p ?w))
?w)) |
succeeds if ?w is the total
weight of all the people on a ?elevator (a variable which must be bound
somewhere else). Note that the value of this fluent depends on who
is on the elevator, not on what their mass is, because in this
formulation it’s assumed not to change. If dieting is to be
taken into account, then we would write
|
(fluent-eval (sum (?p - person ?w - (fluent number))
(and (aboard ?p ?elevator)
(weight ?p ?w))
?w)) |
where now ?w is a fluent
itself.
13 Problems
A problem is what a planner tries to solve. It
is defined with respect to a domain. A problem specifies two
things: an initial situation, and a goal to be achieved. Because
many problems may share an initial situation, there is a facility
for defining named initial situations.
| |
<problem> |
::= (def |
ine (problem <name>) |
|
<situation> |
::= (:situation <initsit name>) |
|
<object
declaration> ::= (:objects
<typed list
(name)>) |
|
<init> |
::= (:init <literal(name)>+) |
|
<initsit name> |
::= <name> |
|
<goal> |
::= |
:action-expansions |
|
|
|
(:expansion <action
spec(action-term)>) |
|
<length-spec> |
::= (:length [(:serial <integer>)] [(:parallel <integer>)]) |
Initial situations are defined thus:
| |
<initsit def> |
::= (def |
ine (situation <initsit name>) |
A problem
definition must specify either an initial situation by name, or a
list of initially true literals, or both. If it specifies both,
then the literals are treated as effects (adds and deletes) to the
named situation. The <initsit
name> must be a name
defined either by a prior situation definition or a prior
problem definition. The
:objects field, if
present, describes objects that exist in this problem or
initial situation but are not declared in the :constants field of its domain or any
superdomain. Objects do not need to be declared if they occur
in the :init list in a
way that makes their type unambiguous.
All predicates which are not explicitly said to
be true in the initial conditions are assumed by PDDL to be false, unless the domain
declares requirement :open-world.
For example,
|
(define (situation briefcase-init)
(:domain briefcase-world)
(:objects P D)
(:init (place home) (place office)))
(define (problem get-paid)
(:domain briefcase-world)
(:situation briefcase-init)
(:init (at B home) (at P home) (at D home) (in P))
(:goal (and (at B office) (at D office) (at P home)))) |
The :goal of
a problem definition may include a goal description or (if the
domain has declare the requirement :action-expansions) an expansion, or both.
A solution to a problem is a series of actions such that (a) the
action sequence is feasible starting in the given inital situation
situation; (b) the :goal, if
any, is true in the situation resulting from executing the action
sequence; (c) the :expansion,
if any, is satisfied by the series of actions (in the sense
explained in Appendix A
).
For instance, in the transportation domain, one
might have the problem
|
(define (problem transport-beans)
(:domain transport)
(:situation standard-network)
(:init (beans beans27)
(at beans27 chicago))
(:expansion (constrained (tag (carry-in-train
beans27 chicago newyork)
(> end))
(in-context end
:precondition (not (spoiled beans27)))))) |
The :requirements field of a problem definition
is for the rare case in which the goal or initial conditions
specified in a problem require some kind of expressiveness that is
not found in the problem’s domain.
The :length
field of a problem definition declares that there is known to be a
solution of a given length; this may be useful to planners that
look for solutions by length.
Unlike addendum names (see
Section 11
), problem names are global.
Exactly how they are passed to a planner is
implementation-dependent.
14 Scope of Names
Here is a table showing the different kinds of
names and over what scope they are bound
| Name type |
Scope |
| Reserved word |
PDDL
language |
| Domain name |
Global |
| Type |
Domain, inherited |
| Constant |
Domain, inherited |
| Domain variable |
Domain, inherited |
| Predicate |
Domain, inherited |
| Action functor |
Domain, inherited |
| Addendum |
Domain, local |
| Situation name |
Domain, inherited |
| Problem name |
Global |
| Method name |
Per action
functor | |
Names with scope “domain, inherited”
are visible in a domain and all its descendants. Names with scope
“domain, local” are visible within a domain but are not
visible in descendant domains. Method names are a documentation
convenience, and need have no scope except that of the functor of
which they are methods.
There is limited possibility of overloading names
in PDDL. The same name may be
used for a global-scope entity (e.g., a problem) and a domain-scope
entity (e.g., a predicate). But the same domain-scoped name cannot
be used for two different kinds of entity. For instance, the same
name cannot be used for a type and an action.
The rules for method names are looser, because
they are not true names. The only restriction is that two distinct
methods for the same action may not have the same name.
15 Current Requirement Flags
Here is a table of all requirements in
PDDL 0.0. Some requirements
imply others; some are abbreviations for common sets of
requirements. If a domain stipulates no requirements, it is assumed
to declare a requirement for :strips.
| Requirement |
Description |
| :strips |
Basic STRIPS-style adds and deletes |
| :typing |
Allow type names in declarations of
variables |
| :disjunctive-preconditions |
Allow or in
goal descriptions |
| :equality |
Support = as
built-in predicate |
| :existential-preconditions |
Allow exists
in goal descriptions |
| :universal-preconditions |
Allow forall
in goal descriptions |
| :quantified-preconditions |
= :existential-preconditions |
|
+ :universal-preconditions |
| :conditional-effects |
Allow when in
action effects |
| :action-expansions |
Allow actions to have :expansions |
| :foreach-expansions |
Allow actions expansions to use foreach |
|
(implies :action-expansions) |
| :dag-expansions |
Allow labeled subactions |
|
(implies :action-expansions) |
| :domain-axioms |
Allow domains to have :axioms |
| :subgoal-through-axioms |
Given axioms p
 q and goal q, generate subgoal p q and goal q, generate subgoal p |
| :safety-constraints |
Allow :safety
conditions for a domain |
| :expression-evaluation |
Support eval
predicate in axioms |
|
(implies :domain-axioms) |
| :fluents |
Support type (fluent t). |
|
Implies :expression-evaluation |
| :open-world |
Don’t make the “closed-world
assumption” for all |
|
predicates -- i.e., if an atomic formula is
not |
|
known to be true, it is not necessarily assumed
false |
| :true-negation |
Don’t handle not using negation as
failure, |
|
but treat it as in first-order logic |
|
(implies :open-world) |
| :adl |
= :strips +
:typing |
|
+ :disjunctive-preconditions |
|
+ :equality |
|
+ :quantified-preconditions |
|
+ :conditional-effects |
| :ucpop |
= :adl +
:domain-axioms |
|
+ :safety-constraints |
16 The Syntax Checker
This section describes how to run the PDDL
syntax checker once you have downloaded the tar distribution file.
The file pddl.system contains a
Kantrowitz-defsystem definition of pddl-syntax-check and pddl-solution-check, which are the syntax
checker and solution checker, respectively. Adjust the directory
names in the calls to MK:DEFSYSTEM, then load in pddl.system, and
do
| (MK:COMPILE-SYSTEM
'PDDL-SYNTAX-CHECK) |
If you compile and load a file full of
PDDL definitions, then the
domain will be defined as you expect. However, this works only if
the file contains no syntactic errors. To find and eliminate
errors, use the function
(PDDL-FILE-SYNCHECK <file>)
This will create a new file with extension
“.chk” which is a
pretty-printed version of the input, with all syntactic errors
flagged thus:
<<
error-description
: thing>>
where ”thing” is a subexpression and
”error-description” says what’s wrong with it.
The idea is that the “.chk” file plays the role of the
“.log” file in
LaTeX. Instead of line numbers the system just prints the entire
input with errors flagged. How well this works depends partly on
the quality of the pretty-printer.
If the global variable STRICT* is set to T, the syntax checker will flag violations
of “strictness” as defined in Section 4.
The syntax checker does a pretty thorough job,
although there are a few gaps. In order to check for correct number
of arguments to predicates and such, it’s necessary to store
information about domains as they are checked, so we have gone all
the way, and written the syntax checker in such a way that it
stores all the information about a domain in various data
structures, whether the checker itself needs the information or
not. Hence a good way to implement a planner that uses the PDDL
notation is to start with the internal data structures containing
the information about a domain, and add whatever indexes the
planner needs for efficiency.
To avoid collisions with users’ code, these
data structures are not stored in any place that is visible by
accident (such as symbol property lists). There is a global hash
table PDDL-SYMBOL-TABLE* that
contains all global bindings. Domains are stored in this table, and
then symbols with domain scope are stored in binding tables
associated with the domain.
17 The Solution Checker
The solution checker is another Lisp program.
To compile and load it, follow the instructions for the syntax
checker, but do (MK:COMPILE-SYSTEM
'PDDL-SOLUTION-CHECK) at the end.
A solution to a PDDL problem is a pair of
items:
- A primitive
action sequence, i.e., a list
of actions that have no expansions.
- A list of
nonprimitive actions, called expansion
hints.
The second component may be absent. The first may,
of course, be empty, but only if the problem is trivial.
Suppose problem P has initial situation S, :goal G, and :expansion E. A solution with action sequence
A and hints H solves P if and only if all of the following are
true:
- A is
feasible starting in situation S, and in the situation resulting
from executing A,
G is true.
- E, and,
if present, H are
executed by some (not necessarily contiguous) subsequence of
A.
- Every action
in A that is declared
:only-in-expansions occurs in
one of the subsequences instantiating E or H.
To run the solution checker, first load the
domain of the problem in (using PDDL-FILE-SYNCHECK), then call
(SOLUTION-CHECK A H P)
where A is the
action sequence, H are the
hints, and P is a problem (or
problem name). It returns T if
it can verify the solution, NIL
if it can’t. It may print some helpful messages as well.
As of Release 1.0, the solution checker does not
actually check for the presence of action expansions. So the
H argument is ignored.
If the problem definition occurs in a file by
itself (pfile), and a solution
occurs in a file by itself (sfile), then the procedure
(SOLUTION-FILE-CHECK sfile pfile)
will read the files, define the problem, and run
SOLUTION-CHECK on the solution
in sfile, which must be in the
form
A Formal Definition of Action Expansions
An anchored action
sequence is a sequence <S0,q1,...,qk>,
where S0 is a situation, q1,...,qk
are ground action terms, and qi+1 is feasible in
the situation resulting from executing q1,...,qi
starting in S0.
We call this situation resultdom(S0,<q1,...,qi>), and define it in the usual
way. The subscript dom
refers to the domain with respect to which result is defined. In what follows,
we will abbreviate resultdom(S0,<q1,...,qi>) as Si.
A realization
within domain dom of an
action spec A
in the anchored action
sequence <S0,q1,...,qk> is a mapping R whose domain is the set of ordered
pairs <E, >, where E is a subexpression of A (defined by position, so two
different occurrences of the same expression count as
different) or an action tag, and
>, where E is a subexpression of A (defined by position, so two
different occurrences of the same expression count as
different) or an action tag, and  is a substitution; and whose range is
a set of unions of closed intervals of the real interval [0,k]. (Not the integer interval!)
is a substitution; and whose range is
a set of unions of closed intervals of the real interval [0,k]. (Not the integer interval!)
A realization R of A
in <S0,q1,...,qk>
satisfies subexpression
E of A with respect
to substitution  , if and only
if one of the following is true:
, if and only
if one of the following is true:
- E is an
action-label term.
- E is an
occurrence of the term (--), and there is some i,0 <
i <
k such that R(E,
 ) = [i,i].
) = [i,i].
- E is a
primitive action term other than (--), and there is some i,1 <
i <
k such that
 (E)
= qi, and R(E,
(E)
= qi, and R(E, ) = [i - 1,i].
) = [i - 1,i].
- E is a
nonprimitive action term, with
 (E)
variable-free, and there is an expansion A' in dom of
(E)
variable-free, and there is an expansion A' in dom of  (E)
(that is, an :expansion
from the :action defining
E or a :method for E), and a realization R' within dom of
(E)
(that is, an :expansion
from the :action defining
E or a :method for E), and a realization R' within dom of  (E)
in <S0,q1,...,qk>, such that R(E,
(E)
in <S0,q1,...,qk>, such that R(E, ) = R'(
) = R'( (E),Ø).
(E),Ø).
- E
=(series E1 ... Em),
and for all i, 1
< i <
m - 1, R satisfies Ei with respect to
 , and for all i,j,1 <
i¡j <
m, and for all
xi
, and for all i,j,1 <
i¡j <
m, and for all
xi  R(Ei,
R(Ei, ),xj
),xj  R(Ej,
R(Ej, ),xi < xj; and R(E,
),xi < xj; and R(E, ) =
) =  1<i<mR(Ei,
1<i<mR(Ei, ).
).
- E
=(parallel E1 ... Em),
and for all 1 < i,j <
m, R satisfies Ei with respect to
 ; and R(E,
; and R(E, ) =
) =  1<i<mR(Ei,
1<i<mR(Ei, ).
).
- E
=(in-context E1 a1 ...al),
and R satisfies
E1 with respect to
 , with R(E,
, with R(E, ) = R(E1,
) = R(E1, ) and,
for each ai:
) and,
for each ai:
- If ai =
:precondition
C, then C is true in SL.
- If ai =
:maintain C, then C is true in Ss
for all integer s
 [L,H].
[L,H].
where L =
min(R(E1, )) and
H = max(R(E1,
)) and
H = max(R(E1, )).
)).
- E
=(choice E1 ... Em),
and for some i, 1
< i <
m, R satisfies Ei with respect to
 , and R(E,
, and R(E, ) = R(Ei,
) = R(Ei, ).
).
- E
=(forsome vars E1),
and there is a substitution
 '
extending
'
extending  by
binding vars, such that
R satisfies E1 with respect to
by
binding vars, such that
R satisfies E1 with respect to  ',
and R(E,
',
and R(E, ) = R(E1,
) = R(E1, ').
').
- E
=(foreach vars P
E1), and there is a set X of extensions to
 such that for all
such that for all  '
' X,
X,  '(P) is ground, such that if
[L,H] = R(E,
'(P) is ground, such that if
[L,H] = R(E, ), then
), then
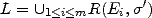 and
and

- E
=(tag l1...ll
E1 ll+1...
lm), and R satisfies E1
with respect to
 , with
R(E,
, with
R(E, ) = R(E1,
) = R(E1, ), and for all
i,1 <
i <
m,
), and for all
i,1 <
i <
m,
- If li =
(<l),
then R(l,
 ) = [L,L].
) = [L,L].
- If li =
(> l), then R(l,
 ) = [H,H].
) = [H,H].
- Otherwise, R(l,
 ) = [L,H].
) = [L,H].
where L =
min(R(E1, )) and
H = max(R(E1,
)) and
H = max(R(E1, )).
)).
- E
=(constrained
E0 E1 ...Em),
and for all i,0
< i <
m, R satisfies Ei with respect to
 and R(Ei,
and R(Ei, )
)
 R(E0,
R(E0, ); and
R(E,
); and
R(E, ) = R(E0,
) = R(E0, ).
).
If R(E, ) is not given a value by repeated
application of the rules in the list, then R(E,
) is not given a value by repeated
application of the rules in the list, then R(E, ) = Ø.
) = Ø.
Finally, an anchored action sequence
satisfies an action spec
if the action spec has a realization into the action sequence
that satisfies the entire action spec.
Note that the formal definition makes
R(E, ) = Ø if there is no occurrence of
E inside a foreach or forsome yielding substitution
) = Ø if there is no occurrence of
E inside a foreach or forsome yielding substitution
 , or if no action corresponding
to E occurs in the action
sequence. Hence if an action spec has references to tags from
contexts that make no sense, they will be interpreted as the
empty set, and be ignored if used in constraints.
(Implementators may not want to implement these semantics.)
, or if no action corresponding
to E occurs in the action
sequence. Hence if an action spec has references to tags from
contexts that make no sense, they will be interpreted as the
empty set, and be ignored if used in constraints.
(Implementators may not want to implement these semantics.)
References

 e
a), where
e is an unextended
PDDL expression and
a is some advice. The
“
e
a), where
e is an unextended
PDDL expression and
a is some advice. The
“
 ” notation indicates
that we are ascending to a “meta” level. The word
“expression” here is interpreted as “any
part of a PDDL expression
that is either a single symbol or an expression of the form
(...).” For
instance, the definition of mov-b given above might be enhanced
for a particular planner thus:
” notation indicates
that we are ascending to a “meta” level. The word
“expression” here is interpreted as “any
part of a PDDL expression
that is either a single symbol or an expression of the form
(...).” For
instance, the definition of mov-b given above might be enhanced
for a particular planner thus: