MLPR w6b - Machine Learning and Pattern Recognition

$$ \newcommand{\D}{\mathcal{D}} \newcommand{\I}{\mathbb{I}} \newcommand{\N}{\mathcal{N}} \newcommand{\bphi}{{\boldsymbol{\phi}}} \newcommand{\bw}{\mathbf{w}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\g}{\,|\,} \newcommand{\nth}{^{(n)}} \newcommand{\te}{\!=\!} \newcommand{\ttimes}{\!\times\!} $$

Bayesian regression

We now revisit regression, fitting real-valued outputs, with a more elaborate statistical approach than before. Previously, we fitted a scalar function, which represented a best guess of an output at a location. Now we will represent a whole probability distribution over possible outputs for each input location. Given this probabilistic model, we can use “Bayesian” reasoning (probability theory) to make predictions. We won’t need to cross-validate as many choices, and we will be able to specify how uncertain we are about the model’s parameters and its predictions. We won’t achieve these advantages in this note, but that’s the motivation for what we’re setting up here.

A probabilistic model for regression

When we created classifiers, it was useful to model the probability distribution over possible labels at each position in input space $P(y\g \bx)$. We can also write down a probabilistic model for regression models. The simplest starting point is a Gaussian model: \[ p(y\g\bx,\bw) = \N(y;\, f(\bx;\bw),\, \sigma_y^2), \] where $f(\bx;\bw)$ is any function specified by parameters $\bw$. For example, the function $f$ could be specified by a linear model, a linear model with basis functions, or a neural network. We have explicitly written down that we believe the differences between observed outputs and underlying function values should be Gaussian distributed with variance $\sigma_y^2$.¹

The starting point for estimating most probabilistic models is “maximum likelihood”, finding the parameters that make the data most probable under the model. Numerically, we minimize the negative log likelihood:² \[\begin{aligned} -\log p(\by\g X, \bw) &= -\sum_n \log p(y\nth\g \bx\nth, \bw)\\ &= \frac{1}{2\sigma_y^2} \sum_{n=1}^N \left[(y\nth-f(\bx\nth;\bw))^2\right] + \frac{N}{2}\log (2\pi\sigma_y^2).\\ \end{aligned}\] If we assume the noise variance $\sigma_y^2$ is constant, we fit the parameters $\bw$ simply by minimizing square error, exactly as we have done earlier in the course.

By following this probabilistic interpretation, we are making more explicit assumptions than necessary to justify least squares³. However, adopting a probabilistic framework can make it easier to explore and reason about different models. For example, if our measuring instrument reported different noise variances $({\sigma_y}\nth)^2$ for different observed $y\nth$ values, we could immediately modify the likelihood and obtain a sensible new cost function. Similarly, we could build a more robust model (as we did for classification) by writing down a noise model with heavier tails to better model outliers. Again, we would immediately obtain a new cost function.

For now we will stay with a simple linear regression model, with known constant noise variance, and look at how to reason about its unknown weight parameters.

Representing uncertainty with distributions

[If this section doesn’t make sense, just keep reading. It’s just meant as motivation, and the next section is more concrete. Most people need to see a few restatements of Bayesian learning before it makes sense.]

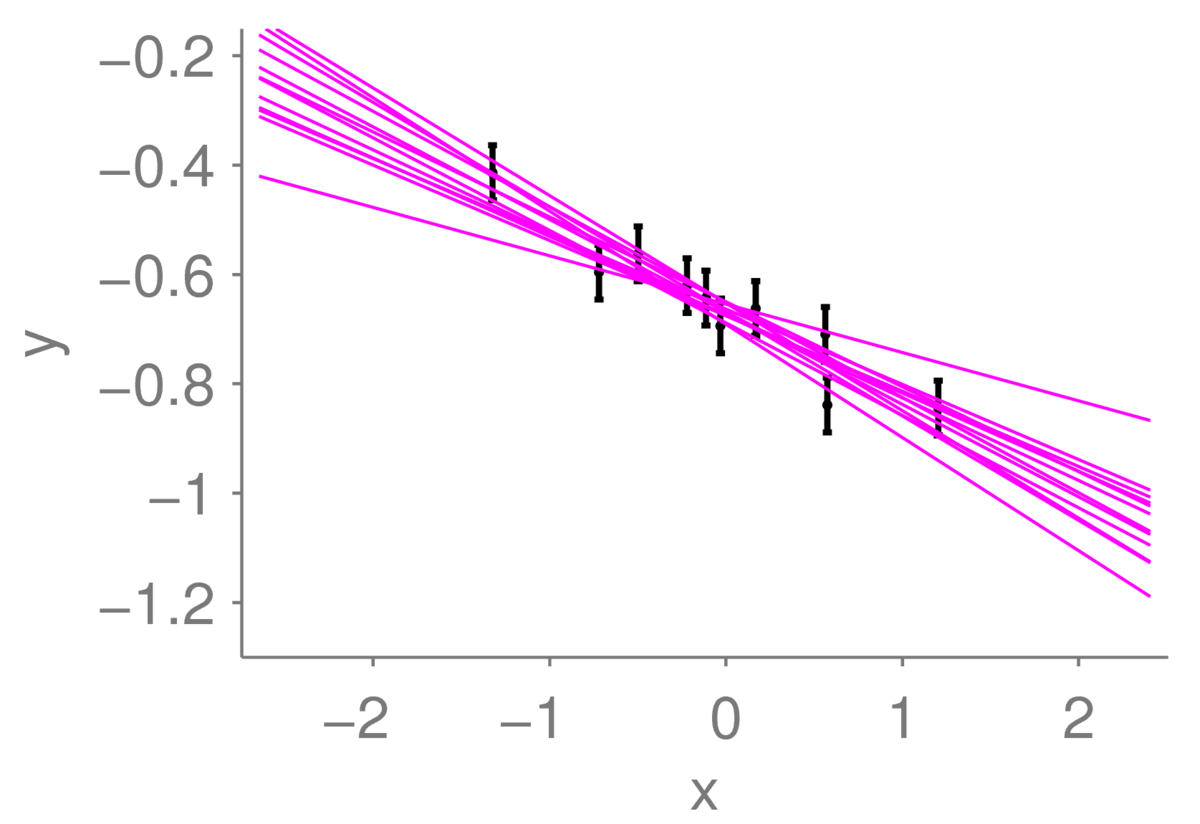
As a physics undergraduate I plotted experimental results, with error bars, in a paper lab book. We were instructed to find a line of best fit by eye, and draw it using a pencil and ruler. We’d also draw the steepest and shallowest straight lines that were still reasonably good fits to the data, to get a sense for how uncertain the original fit was. Given $\pm \sigma_y$ error bars on our observed $y$ values, we wanted each fitted line to go through about 2/3 of the error bars. But there are many ways to draw such a line: with limited noisy observations, we can’t know where an underlying function is.

What I’ve done in the figure below is slightly different. Rather than just showing extreme lines, I’ve drawn a selection of twelve lines, each of which could plausibly have generated the data. If I included the line that I actually used to generate the data in this collection, you would have trouble identifying which one it was with certainty.

One of the lines does look somewhat less plausible than the others. But it could be close to the true line: maybe the left-most observation happened to have a large amount of noise added to it, and the line is less steep than you think.

If we observe a lot more points, we can be more certain where the underlying line is. The range of plausible lines we might draw should become more limited, perhaps like this:

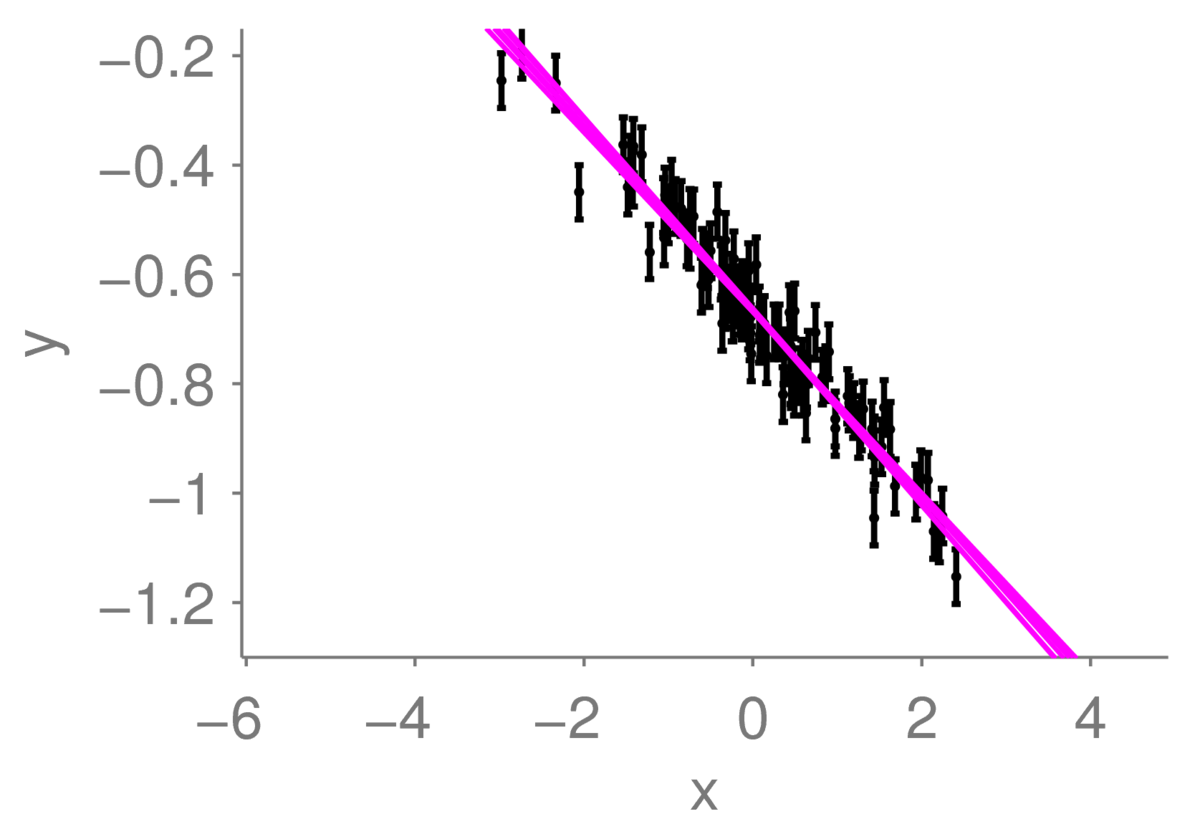
I’ve drawn the lines almost on top of each other, so they appear as one thick line. I am fairly certain that the true function is somewhere within that tight collection of lines.

If we wanted an intelligent agent to draw these plausible lines of fit for us, how should it do it? Or more generally, how can we systematically express the uncertainty that we should have in conclusions based on limited and noisy data?

One formal approach to handling uncertainty is to use probability distributions to represent our beliefs, and probability theory to update them.⁴

In the context of line fitting, beliefs are represented by a probability distribution over the parameters. When we are fairly certain, the distribution over parameters should have low variance, concentrating its probability mass on a small region of parameter space. Given only a few datapoints, our distribution over plausible parameters should be much broader.

In the figures above, I drew samples from probability distributions over parameters, and plotted the resulting functions. The lines show just twelve of the many reasonable explanations of the data as represented by a distribution over the model parameters. I got the distributions from Bayes’ rule as described in the next section.

Bayes’ rule for beliefs about parameters

To apply probability theory to obtain beliefs we need both a probabilistic model, and prior beliefs about that model.

Our example model for a straight line fit is: \[ f(x;\bw) = w_1x + w_2, \qquad p(y\g x,\bw) = \N(y;\,f(x;\bw),\sigma_y^2). \] If we knew the parameters $\bw$, we could compute the function for any $x$ and simulate what typical observations at that location would look like. However, when learning from data, we don’t know the parameters $\bw$.

The prior

Our prior beliefs are represented by a distribution over the parameters, specifying which models we think are plausible before observing any data. For example, if we set: \[ p(\bw) = \N(\bw;\,\mathbf{0},0.4^2\I), \] we think the following functions are all reasonable models we could consider:

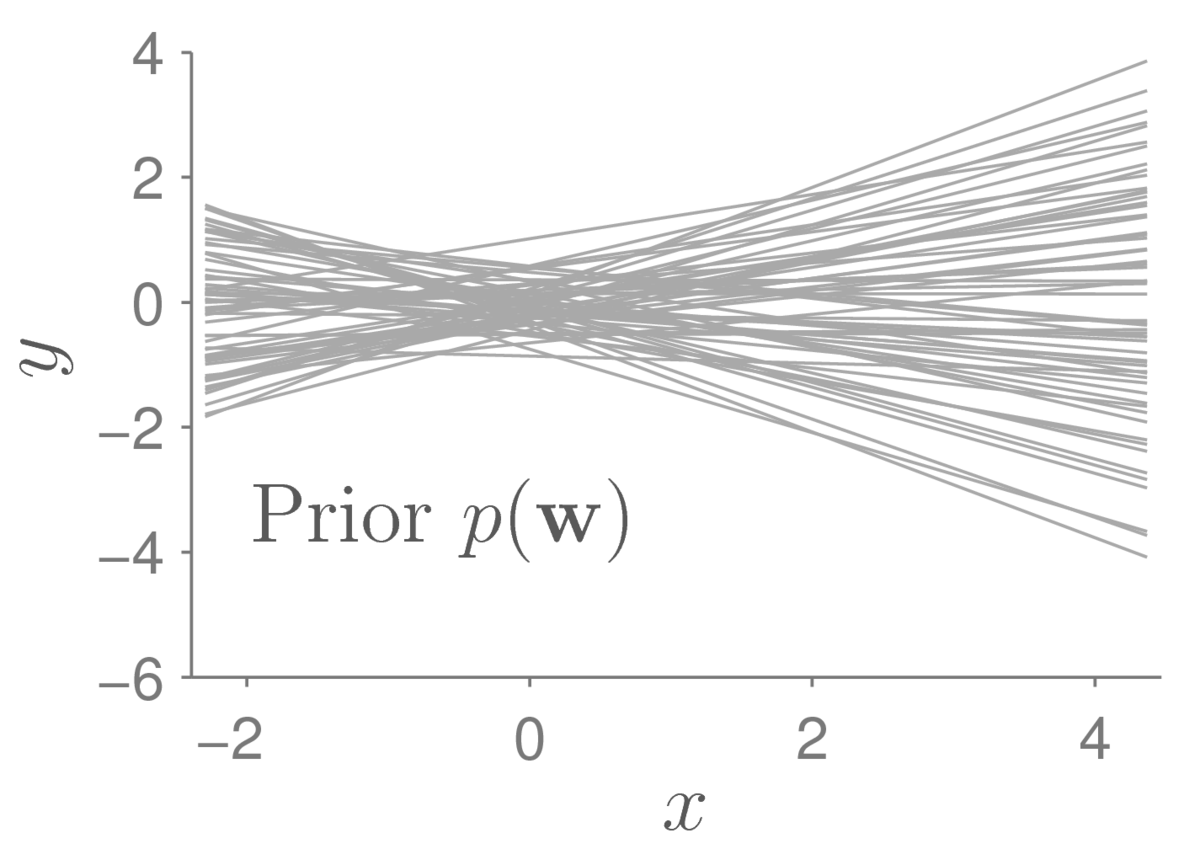
Each of the lines above is a function $f(x;\bw)$ where I have sampled the parameters $\bw$ from the prior distribution. They are quite bunched up around the origin. If I wanted to consider larger intercepts at $x\te0$, I could pick a broader prior on the bias parameter $w_2$.

The posterior

The posterior distribution gives the beliefs about the model parameters that we should have after observing data $\D\te\{\bx\nth,y\nth\}$. These beliefs are represented by the distribution $p(\bw\g \D)$, pronounced “p of $\bw$ given $\D$”, and are obtained by Bayes’ rule. For generic data $\D$ we’d write: \[ p(\bw\g \D) = \frac{p(\D\g\bw)\,p(\bw)}{p(\D)} \propto p(\D\g\bw)\,p(\bw). \] However, for regression we often treat our data as $\by\te\{y\nth\}$, and condition on the inputs $X\te\{\bx\nth\}$ as fixed known quantities that don’t effect our prior beliefs. With these assumptions we would instead write: \[ p(\bw\g \D) = p(\bw\g\by, X) = \frac{p(\by\g\bw,X)\,p(\bw)}{p(\by\g X)} \propto p(\by\g\bw, X)\,p(\bw). \] Bayes’ rule reweights or updates the prior distribution, so that parameters that are more compatible with the data become more probable.

Applying Bayes rule to our toy regression problem (skipping the maths of how to do it for the moment) gives beliefs centred around models that fit the observed data-points. Sampling from that distribution gives the plot below:

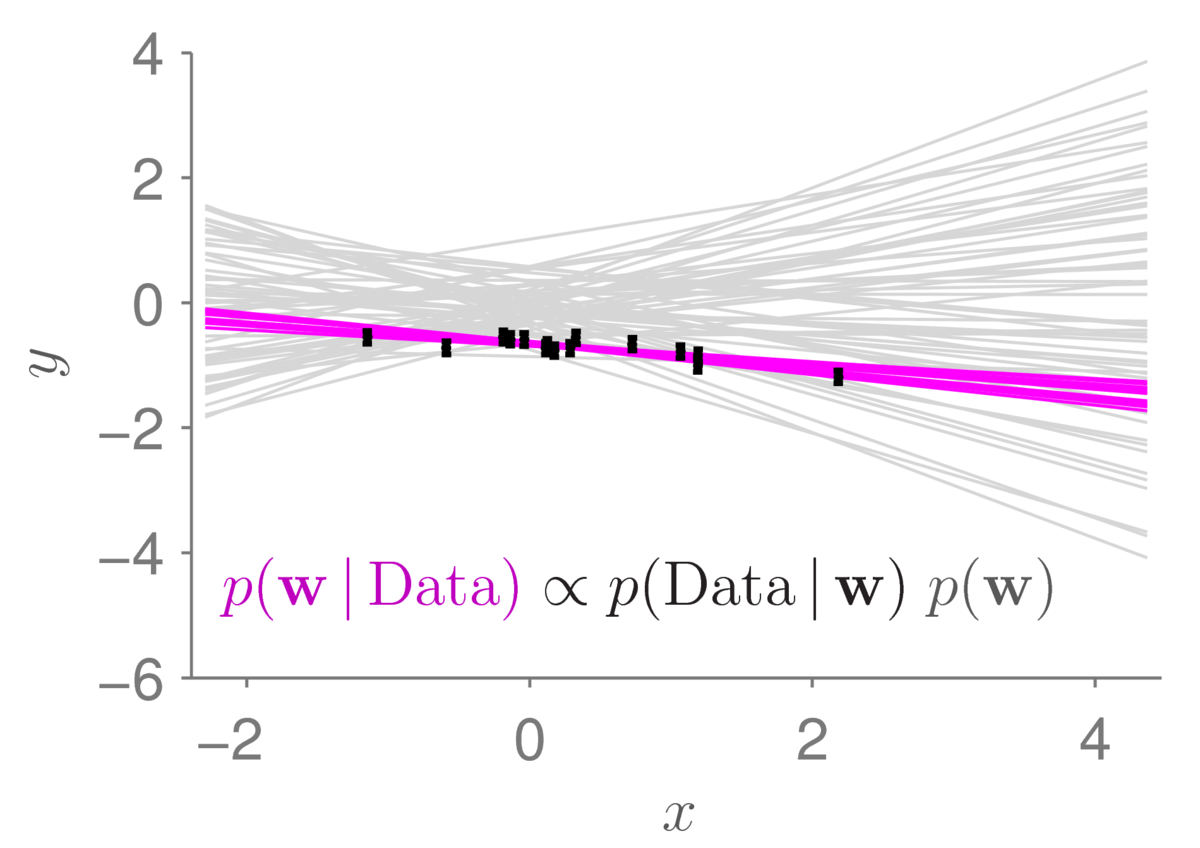
The light gray lines show the samples from the prior distribution that we had before. The small black bars show data points (with error bars). The magenta lines show 12 samples from the posterior distribution. As is usually the case (if our data is useful), the posterior distribution concentrates in a much smaller region of parameter space than the prior. The corresponding straight-line functions are also less spread out. Under the posterior, we only believe that lines passing close to the data are plausible.

Zooming in to the same diagram, we can get a better view of the data and the possible models sampled from the posterior distribution:

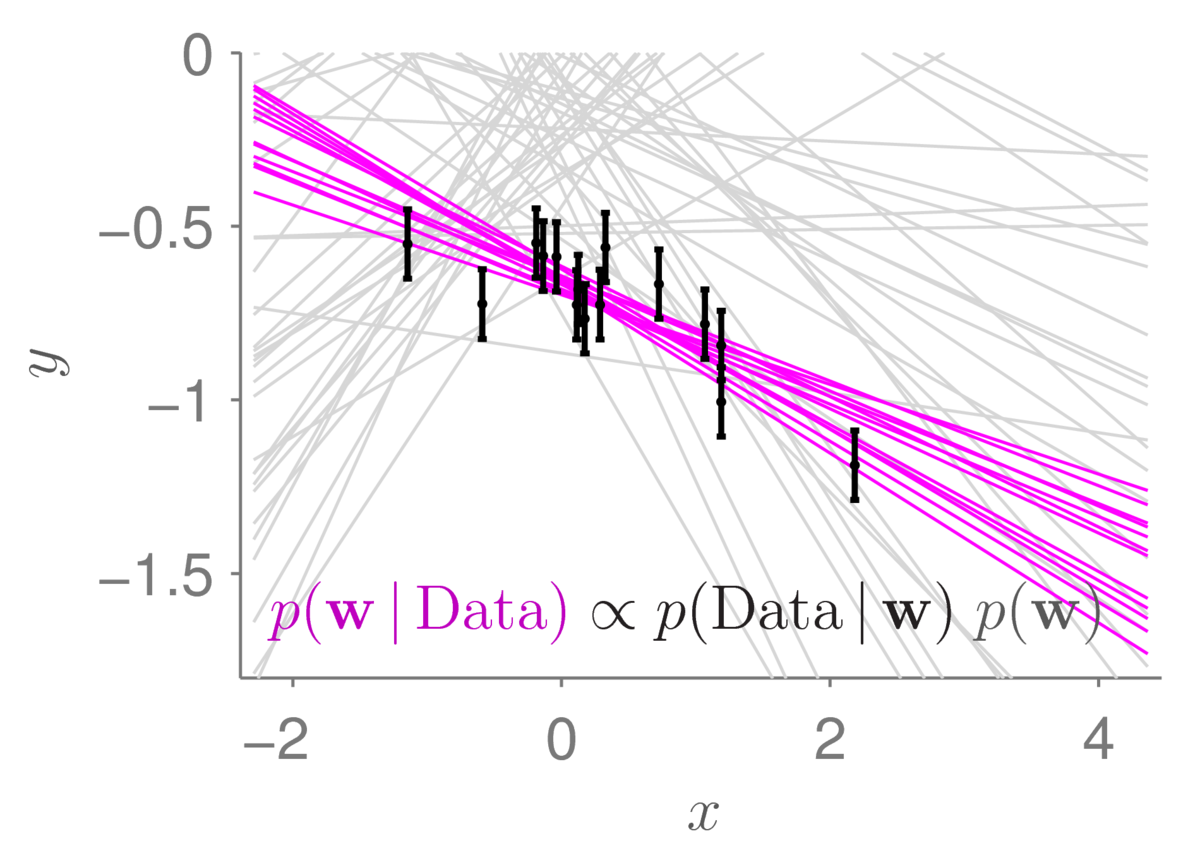
The plausible lines sampled from the posterior distribution naturally spread out as we move away from the observed data. The statistical machinery automatically tells us that we are less certain about where the function is as we move away from where we have measured it.

Computing the Posterior

For general models, the posterior distribution won’t have a convenient form that we can represent with a few parameters. The likelihood is a product of $N$ terms for $N$ datapoints, and that product could potentially create a complicated function.

A conjugate prior is one where the product of the prior and likelihood combines to give a distribution with the same functional form as the prior. A Gaussian prior over linear regression weights is conjugate to its linear-Gaussian likelihood, and we obtain a Gaussian posterior: \[\begin{aligned} p(\bw\g \D) &\propto p(\bw)\,p(\by\g\bw, X),\\ &\propto \N(\bw;\,\mathbf{0},\,\sigma_w^2\mathbb{I})\,\prod_n \N(y\nth;\bw^\top\bphi(\bx\nth),\, \sigma_y^2),\\ &\propto \N(\bw;\,\mathbf{0},\,\sigma_w^2\mathbb{I}) \,\N(\by;\,\Phi\bw,\, \sigma_y^2\I), \end{aligned}\] where $\bphi(\bx)$ is an augmented input vector as in earlier notes, for example $\bphi(x) = [x~~1]^\top$ for fitting a straight line with scalar inputs. As before, $\Phi$ is a matrix with these augmented vectors in the rows. Here I’ve assumed a zero-mean prior, and a spherical prior covariance. In Murphy’s notation for the prior parameters: $\bw_0\te\mathbf{0}$ and $V_0\te\sigma_w^2\mathbb{I}$, which set our beliefs after observing 0 datapoints. We could set the prior mean $\bw_0$ and covariance $V_0$ to other values, for example to allow the “bias” parameter that specifies the intercept to vary more.

The posterior is proportional to the exponential of a quadratic in $\bw$, which means it is a Gaussian distribution. Murphy writes the answer in the form: $p(\bw\g\D)\te\N(\bw;\,\bw_N, V_N)$, the beliefs after observing $N$ datapoints. As in a tutorial exercise, we can identify the posterior mean $\bw_N$ and covariance $V_N$ from the linear and quadratic coefficients of $\bw$ inside the exponential. It’s just linear algebra grunt work, which results in: \[\begin{aligned} V_N &= \sigma_y^2(\sigma_y^2V_0^{-1} + \Phi^\top \Phi)^{-1}\\ \bw_N &= V_N V_0^{-1}\bw_0 + \frac{1}{\sigma_y^2}V_N \Phi^\top\by. \end{aligned}\] Or replace $\Phi$ with $X$ if you haven’t applied a basis function transformation. I am not expecting you to memorize these expressions!