OOP Lab 7 Exercises: Logic and Computation
| Authors: | Ewan Klein
Jonathan Abourbih |
|---|---|
| Version: | 1.14 |
| Date: | 2009-03-02 |
Contents
Problems?
If any of the following exercises are unclear or seem to contain errors, please don't hesitate to let us know! Just send an email.
Preamble
This week's lab exercises have a logical slant and again focus on class hierarchies. Please make sure that you have read Chapters 7, 8 and 9 the textbook Head First Java.
Exercises
Exercise 1: A Fine Proposition
Most of you should have encountered propositional logic in the Logic and Computation course last semester. In this exercise, you will represent formulas of propositional logic in Java and develop methods for displaying them as strings and calculating their semantic value. Setting up this exercise needs a fair bit of background, so please bear with us.
Here is a set of inductive rules for the language of propositional logic:
- There is a finite set PropConstant of propositional constants, written P, Q, R, etc.
- Every expression in PropConstant is also in Wff (i.e, the set of Well Formed Formulas).
- If a formula A is in Wff, then so is ~A (i.e., not A).
- If the formulas A and B are in Wff, then so are
- A & B (i.e., A and B),
- A | B (i.e., A or B),
- A -> B (i.e., A implies B),
- A <-> B (i.e., A if and only if B).
- Nothing else is in the set Wff.
Wff is defined as an interface since both of its methods are abstract.
/**
* The interface for Wffs for Propositional Logic.
* They have to be eval-able and print out in sensible way.
*
* @author Ewan Klein <ewan@inf.ed.ac.uk>
*/
public interface Wff {
public boolean eval(Valuation val);
public String toString();
}
The methods toString() and eval() will need to be implemented by every class which implements the interface.
The class PropConstant is our first subclass of Wff, and provides the basis for the induction. The definition includes a constructor whose parameter is a String; we use this to turn a string P into an instance of PropConstant. Thus, we can say things like PropConstant p = new PropConstant("P");.
/**
* @author Ewan Klein <ewan@inf.ed.ac.uk>
*
*/
public class PropConstant implements Wff {
private String propConstant;
public PropConstant(String str) {
this.propConstant = str;
}
public String toString() {
return propConstant;
}
/**
* Evaluate by looking up the instance in the Valuation
*
* @param val the Valuation
*/
public boolean eval(Valuation val) {
return val.get(this);
}
}
The method toString() simply returns the string we used in inialization. We'll return to the eval() method in a while.
What next? Rather than looking at negated formulas (since these are one of a kind), let's think about how to handle the Wffs defined in clause (4) above. There are various approaches we could adopt, but our choices become more constrained when we think about evaluation. Suppose we want to evaluate a Wff such as P & Q. Whether it is true or false depends on the truth values of the propositional constants P and Q and on the truth conditions for &. Now, the semantic value of the propositional constants can vary from situation to situation. Let's say that a Valuation is a mapping from propositional constants to truth values and each Valuation corresponds to the way the world could be. How are we going to model this in Java? As a HashMap of course! Valuation is little more than a convenient wrapper for a HashMap:
/**
* A Valuation for Propositional Constants,
* associating them with truth values
*/
import java.util.HashMap;
public class Valuation {
HashMap<PropConstant, Boolean> val = new HashMap<PropConstant, Boolean>();
public boolean get(PropConstant propConstant) {
return val.get(propConstant);
}
public Boolean put(PropConstant propConstant, boolean tv) {
return val.put(propConstant, tv);
}
}
(Note that Boolean is the class corresponding the primitive type boolean. Values get automatically converted between these two types as appropriate when they get added to, or returned from, the HashMap.)
So this is going to allow us to create a Valuation instance and then add specific truth values for specific PropConstants.
Let's think about propositional formulas such as A & B versus A | B. Each of them contains a leftmost Wff, a binary operator, and a rightmost Wff. From a semantic point of view, what matters most in distinguishing the two types of Wff is the meaning of the operator, & versus |. So let's think of this meaning as being local to the particular class of each formula. In other words, we want to define two types of Wff, which we will call AndWff and OrWff. Since these have some things in common, we'll make them both subclasses of a second abstract class, BinaryWff. However, we also want to control the syntactic aspects of complex Wffs, by listing the allowed operators. To do this, we will use Java's enum type, as illustrated in Operator.java
/**
* An enumeration class of boolean operators for Propositional Logic. These end
* up being like constants.
*/
public enum Operator {
/**
* Initialise each operator with its respective symbol
*/
NEG("~"), AND("&"), OR("|"), IMP("->"), IFF("<->");
private String symbol;
/**
* Constructor for the class
*
* @param symbol
* the formal symbol used for the operator
*/
Operator(String symbol) {
this.symbol = symbol;
}
public String toString() {
return symbol;
}
}
You can find out more about Java Enumerations on pages 671-673 of HFJ.
PropLogicLauncher should give you more of an overview of how everything works:
public class PropLogicLauncher {
public static void main(String[] args) {
// Make some new constants
PropConstant p = new PropConstant("P");
PropConstant q = new PropConstant("Q");
PropConstant r = new PropConstant("R");
// Build some Wffs
Wff e0 = new NotWff(p);
Wff e1 = new AndWff(q, e0);
Wff e2 = new OrWff(e1, p);
Wff e3 = new IfWff(e1, p);
Wff e4 = new NotWff(e2);
// What does their toString() method produce?
System.out.println("Display form of Wff e0 is: " + e0);
System.out.println("Display form of Wff e1 is: " + e1);
System.out.println("Display form of Wff e2 is: " + e2);
System.out.println("Display form of Wff e3 is: " + e3);
System.out.println("Display form of Wff e4 is: " + e4);
System.out.println();
// Create a Valuation and set some truth values
Valuation val = new Valuation();
val.put(p, true);
val.put(q, false);
val.put(r, true);
// Compute the truth values and display the results
System.out.println("The value of Wff e0 is: " + e0.eval(val));
System.out.println("The value of Wff e1 is: " + e1.eval(val));
System.out.println("The value of Wff e2 is: " + e2.eval(val));
System.out.println("The value of Wff e3 is: " + e3.eval(val));
System.out.println("The value of Wff e4 is: " + e4.eval(val));
}
}
Here's the output:
Display form of Wff e0 is: ~P Display form of Wff e1 is: (Q & ~P) Display form of Wff e2 is: ((Q & ~P) | P) Display form of Wff e3 is: ((Q & ~P) -> P) Display form of Wff e4 is: ~((Q & ~P) | P) The value of Wff e0 is: false The value of Wff e1 is: false The value of Wff e2 is: true The value of Wff e3 is: true The value of Wff e4 is: false
Let's think about what needs to happen when we call e1.eval(val). The "abstract syntax" of e1 is as follows:
AndWff(PropConstant("Q"), NotWff(PropConstant("P")))
When we call eval(val) on e1, we need to figure out the truth values of its two subexpressions, namely:
PropConstant("Q")
and:
NotWff(PropConstant("P")).
In order to compute PropConstant("Q").eval(val), we just have to look up the truth value of PropConstant("P") in our Valuation val (which yields the value false), and we then hand this value back up to the call e1.eval(val). In order to compute:
NotWff(PropConstant("P")).eval(val)
we first have to compute:
PropConstant("P").eval(val)
and again we need to look up the truth value of PropConstant("P") in our Valuation val (which yields the value true). We hand this value back up to the call NotWff(PropConstant("Q")).eval(val), which we can think of as computing the value of the Java expression ! true, yielding false. So now:
AndWff(PropConstant("Q"), NotWff(PropConstant("P"))).eval(val)
is reduced to evaluating something like the Java expression false && false, yielding the result false.
This is a standard example of recursive evaluation. We call the eval() method on the top-level expression e1, keep on working our way down until we hit the propositional constants where the recursion bottoms-out, and then work our way up again up, plugging values into the subexpressions until we get to top-level.
Here is a partial implemtation of AndWff :
/**
* The class of conjunctive Wffs for Propositional Logic
*/
public class AndWff extends BinaryWff {
/**
* Call the constructor of the superclass (BinaryWff)
*
* @param left the left sub-Wff
* @param right the right sub-Wff
*/
AndWff(Wff left, Wff right) {
super(left, right);
setOp(Operator.AND);
}
/**
* Recursively evaluate this Wff by evaluating the sub-Wffs
*
* @param val the Valuation that is passed down to Propositional Constants
*/
public boolean eval(Valuation val) {
// complete this so that A & B gets the right truth conditions
}
}
Tasks:
Create an abstract class BinaryWff which implements Wff. AndWff inherits the following methods which are implemented in BinaryWff:
- setOp() -- a standard setter to set the logical operator
- getLeft() and getRight() -- get the left and right sub-Wffs
- toString() -- return the string format for any binary Wff
BinaryWff will also contain this constructor and the corresponding instance variables:
public BinaryWff(Wff left, Wff right) { this.left = left; this.right = right; }Complete the implementation of AndWff.
Create similar subclasses of BinaryWff to deal with OrWff (disjunctions) and IfWff (implications). Make sure you override the eval() method appropriately.
Create the class NotWff as an implementation of Wff, and again make you override the eval() method appropriately.
Create a JUnit test file that tests that your Wffs get printed out in the correct manner and the truth conditions are computed correctly for each logical operator.
Submit your code for BinaryWff, AndWff, OrWff, IfWff and NotWff to Web-CAT in the usual way.
OPTIONAL Exercise 2: DIY Calculator
In this exercise, we're going to focus on the beginnings of a pocket calculator. Our pocket calculator will be very simple, and only support addition, subtraction, multiplication, and division. Also, since the calculator will be incredibly cheap, it does not care about order-of-operations. Calculations are performed in the sequence that they are entered.
In general, it would be possible to have an implementation in a monolithic class, like:
public class Calculator {
public int add(int a, int b) {
return a + b;
}
//etc...
}
But that's not very extensible. Think about what would happen if we needed to add another operation in the future. The most obvious answer would be simply to add a new method to the Calculator class. But what if you don't have access to the source code for Calculator? In that case, you might want to extend it, like:
public class BetterCalculator extends Calculator {
public int pow(int a, int b) {
// implementation...
}
}
This may not seem like a problem, but in the real-world this makes for messy implementations that are very hard to maintain. Especially if you keep adding operations over the years. Imagine the inheritance hierarchy! In general, we don't do this. Instead, it's typically easier to compose multiple operations into a single expression. An example UML design appears below:
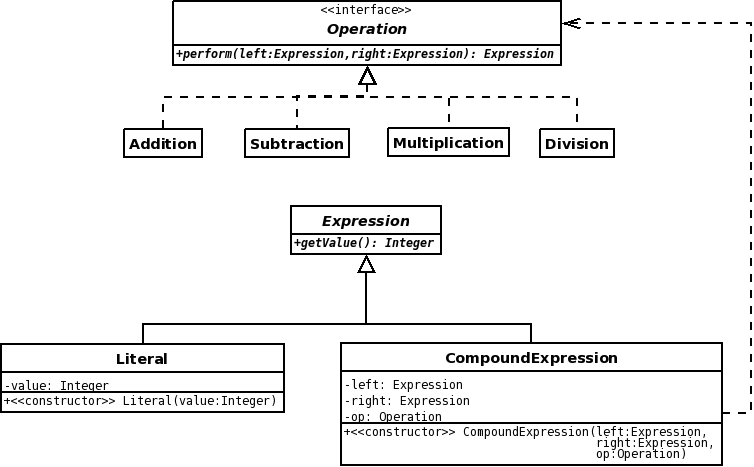
If you're not familiar with some of the notation in the diagram, you may find the UML Cheatsheet at http://www.loufranco.com/blog/assets/cheatsheet.pdf useful.
Your task is to implement a calculator that follows this design. Submit all your code as a zip archive to Web-CAT. It should pass the JUnit test cases in CalcTest :
import junit.framework.TestCase;
public class CalculatorTest extends TestCase {
protected void setUp() throws Exception {
super.setUp();
}
public void testOperationAdd() throws Exception {
Operation a = new Addition();
assertEquals(8, a.perform(new Literal(5), new Literal(3)));
assertEquals(0, a.perform(new Literal(0), new Literal(0)));
}
public void testOperationSubtract() throws Exception {
Operation s = new Subtraction();
assertEquals(15, s.perform(new Literal(29), new Literal(14)));
assertEquals(-1, s.perform(new Literal(0), new Literal(1)));
}
public void testOperationMultiply() throws Exception {
Operation m = new Multiplication();
assertEquals(15, m.perform(new Literal(3), new Literal(5)));
assertEquals(0, m.perform(new Literal(0), new Literal(934)));
}
public void testOperationDivide() throws Exception {
Operation d = new Division();
assertEquals(15, d.perform(new Literal(30), new Literal(2)));
assertEquals(0, d.perform(new Literal(0), new Literal(100)));
try {
d.perform(new Literal(100), new Literal(0));
fail();
} catch (ArithmeticException ae) {
// do nothing
}
}
public void testLiteral() throws Exception {
assertEquals(20, new Literal(20).getValue());
assertEquals(0, new Literal(0).getValue());
assertEquals(-100, new Literal(-100).getValue());
}
public void testCompoundExpression() throws Exception {
Expression ce = new CompoundExpression(new Literal(5), new Addition(), new Literal(100));
assertEquals(105, ce.getValue());
Expression ce1 = new CompoundExpression(ce, new Multiplication(), new Literal(5));
assertEquals(525, ce1.getValue());
Expression ce2 = new CompoundExpression(ce1, new Division(), new Literal(25));
assertEquals(21, ce2.getValue());
Expression ce3 = new CompoundExpression(ce2, new Subtraction(), new Literal(20));
assertEquals(1, ce3.getValue());
}
}