University Homepage School Homepage School Contacts School Search

Categories and Quantum Informatics Lab

In this lab we will verify the correctness of the Steane code. This is a quantum error correcting code: by encoding 3 logical qubits in 7 physical qubits using redundancy, we can recover from correct from single X and Z errors in case the underlying physical qubits are faulty. Hit the wikipedia page and read up a bit on error correcting codes.

To do this verification, we will be using QuantoMatic. This is a software tool that helps to rewrite diagrams in the graphical calculus, and can even find some proofs automatically. Fire it up:

  /opt/QuantoDerive/quanto-derive.sh

First work through the tutorial on the quantomatic website.

We will follow this article. Start by inputting the equational rules of the ZX-calculus, as specified on page 5. You can cheat a bit by downloading the ZX-project.

This is the encoder for the Steane code, as a quantum circuit:

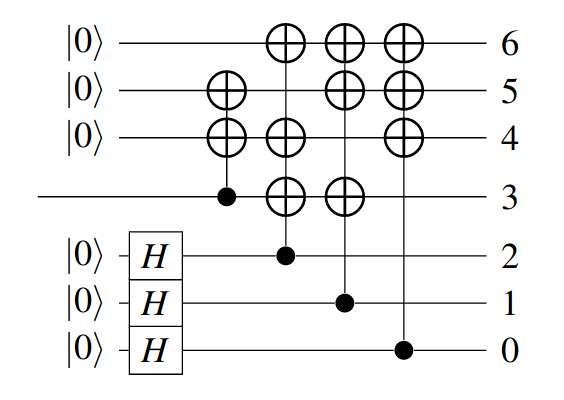
Import it as a graph in quantomatic:

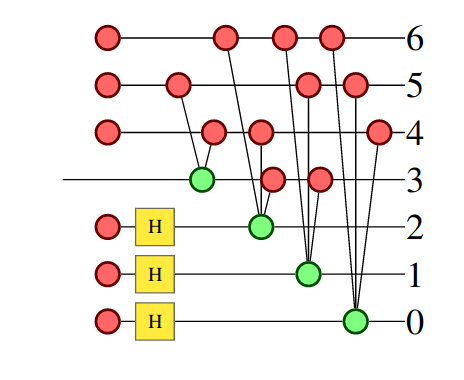
The decoder is just the dagger of this graph, i.e. its left-right mirror image.

Now for the error corrector, as a quantum circuit:

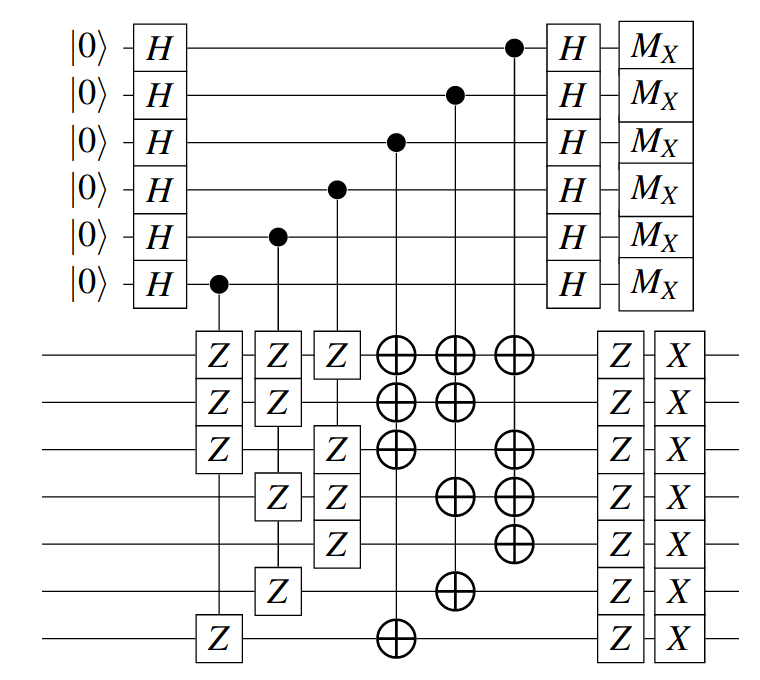
Import it as a graph:

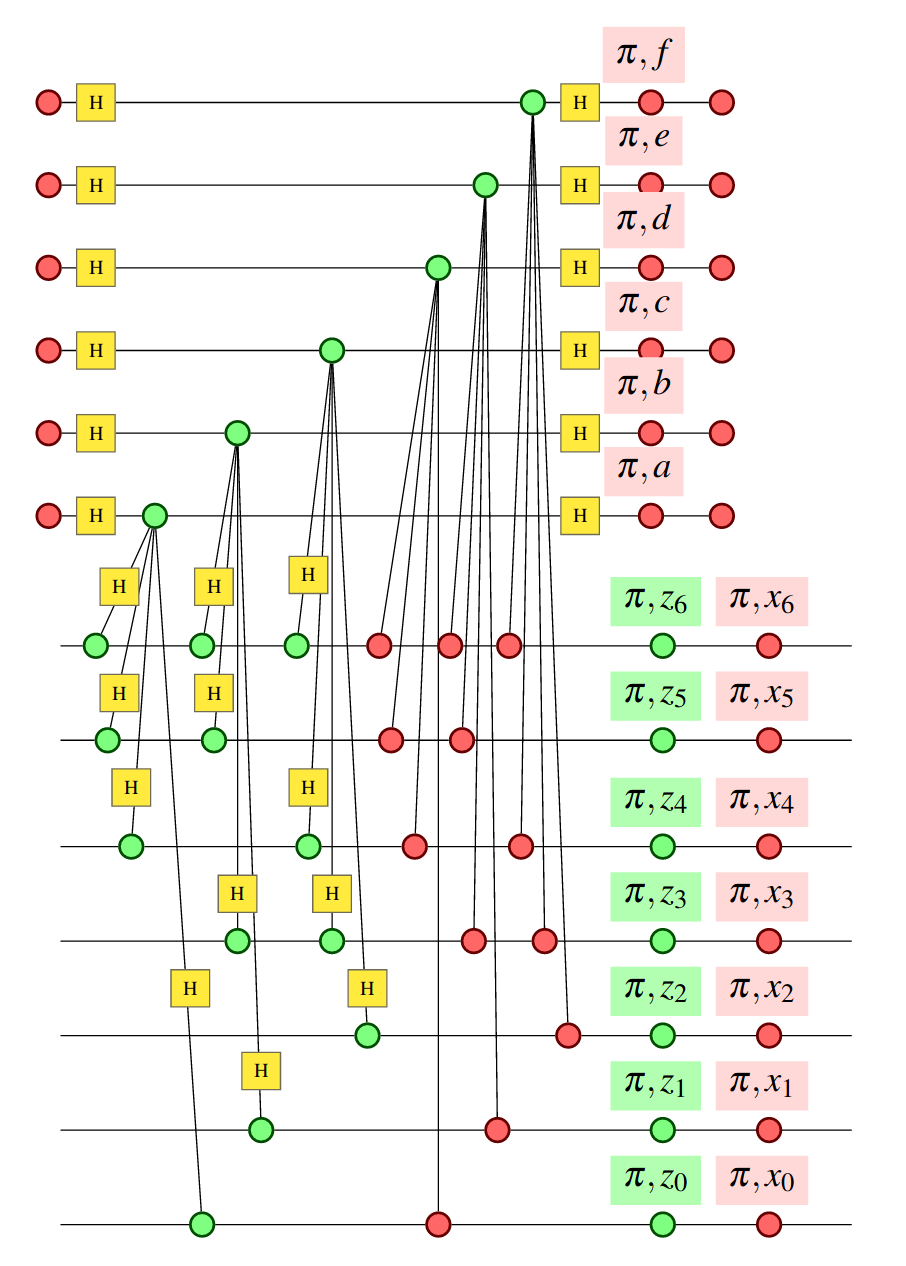
Compose the encoder with the corrector and the decoder, and (have quantomatic) prove that this indeed gives the identity!

Bonus: formalise a single-qubit X error, and (have quantomatic) prove that the corrector can recover from it. Do the same for a single-qubit Z error.

["Answers"]