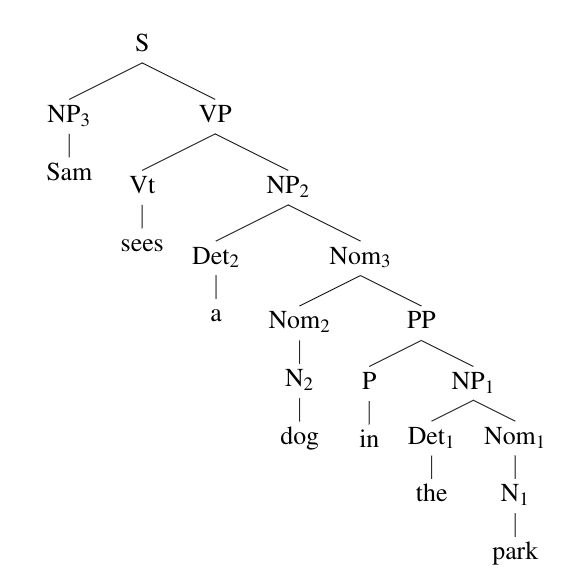
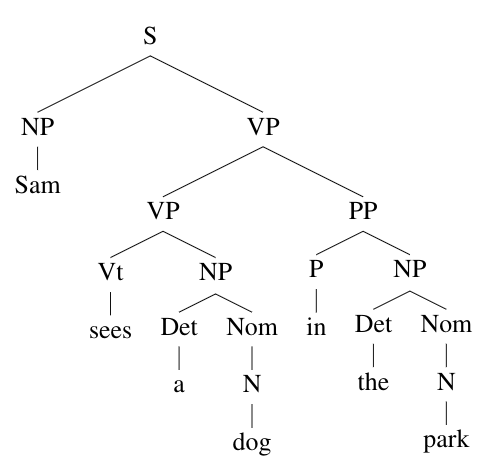
The syntactic trees are:
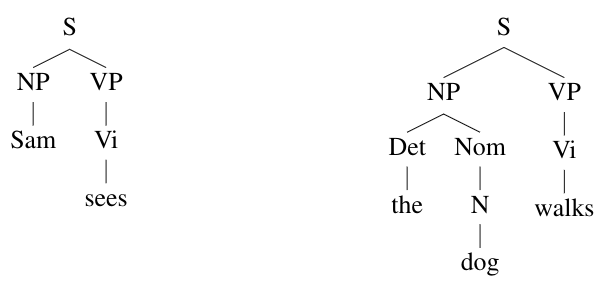
In the first tree, the meanings attached to each tree node are as follows:
Sam, NP: \(\lambda P. P(Sam)\)
sees, Vi, VP: \(\lambda x. \exists e. seeing(e) \wedge seer(e, x)\)
S: derived as NP.sem(VP.sem), which is \[\begin{aligned} (\lambda P. P(Sam))[\lambda x. \exists e. seeing(e) \wedge seer(e, x)] &= (\lambda x. \exists e. seeing(e) \wedge seer(e, x))[Sam]\\ &= \exists e. seeing(e) \wedge seer(e, Sam)\end{aligned}\]
I’ve added a little more notation to keep things clear: I put round brackets around the lambda expression that’s about to undergo lambda reduction, and square brackets around the expression that’s about to be substituted in place of the lambda variable. This will help especially with more complicated reductions below.
In the second tree, the meanings attached to each tree node are as follows:
the, Det: \(\lambda P. \lambda Q. \exists! x. P(x) \wedge Q(x)\)
dog, N, Nom: \(\lambda x. dog(x)\)
walks, Vi, VP: \(\lambda x. \exists e. walking(e) \wedge walker(e,x)\)
NP (the dog): derived as Det.sem(Nom.sem), which is \[\begin{aligned} (\lambda P. \lambda Q. \exists! x. P(x) \wedge Q(x))[ \lambda x. dog(x)] &= (\lambda P. \lambda Q. \exists! x. P(x) \wedge Q(x))[ \lambda y. dog(y)] \\ &= \lambda Q. \exists! x. (\lambda y. dog(y))[x] \wedge Q(x)\\ &= \lambda Q. \exists! x. dog(x) \wedge Q(x) \end{aligned}\] I did something important in the first line: before I substituted \(\lambda x.dog(x)\) in for \(P\), I re-named the variable \(x\) in the substituted expression and called it \(y\). That’s because there was already an \(x\) in the outer expression. In this case, those \(x\)’s turn out to refer to the same thing, but that isn’t guaranteed to be the case. If I didn’t re-name the variable, I might have ended up making two variables that are supposed to refer to different things actually refer to the same thing. (This is basically a namespace issue, just like what happens when you define a variable inside a function in Python with the same name as one outside the function: implicitly, Python treats them as two different things. Here we have to rename one of them explicitly to avoid clashes.)
S: derived as NP.sem(VP.sem), which is \[\begin{aligned} & (\lambda Q. \exists! x. dog(x) \wedge Q(x))[\lambda x. \exists e. walking(e) \wedge walker(e,x)]\\ &= \exists! x. dog(x) \wedge (\lambda y. \exists e. walking(e) \wedge walker(e, y))[x]\\ &= \exists! x. dog(x) \wedge \exists e. walking(e) \wedge walker(e, x)\end{aligned}\] Again, notice that I re-named the \(x\) in the “walk” part in the second line.
The problem is that the semantic attachment for VP says that the Vt takes the NP as its argument. But all our NPs have meanings like \(\lambda P. (\ldots\)). If we apply the proposed simple (base-form) MR for see to something like that, we substitute the complex NP MR for \(y\) and end up with an invalid FOL expression. The solution is to type-raise the MRs for transitive verbs, just as we saw type-raising for NPs in lecture. This allows the Vt to take its NP argument and apply that NP to the base meaning of the Vt. For example, the MR for walks Spot is derived as follows. \[\begin{aligned}
& (\lambda P \lambda x. P(\lambda y. \exists e. walking(e) \wedge walker(e, x) \wedge walkee(e, y))[\lambda P. P(Spot)] \\
&=(\lambda P \lambda x. P(\lambda y. \exists e. walking(e) \wedge walker(e, x) \wedge walkee(e, y))[\lambda Q. Q(Spot)]) \\
&= \lambda x. (\lambda Q. Q(Spot))[\lambda y. \exists e. walking(e) \wedge walker(e, x) \wedge walkee(e, y)] \\
&= \lambda x. (\lambda y. \exists e. walking(e) \wedge walker(e, x) \wedge walkee(e, y))[Spot] \\
&= \lambda x. \exists e. walking(e) \wedge walker(e, x) \wedge walkee(e, Spot) \\
\end{aligned}\]
We just showed how to compute the meaning of the VP in ``Sam walks Spot’’. We can combine it with the subject NP using the NP.sem(VP.sem) attachment as follows: \[\begin{aligned} & (\lambda P. P(Sam))[\lambda x. \exists e. walking(e) \wedge walker(e, x) \wedge walkee(e, Spot)]\\ &= (\lambda x. \exists e. walking(e) \wedge walker(e, x) \wedge walkee(e, Spot))[Sam]\\ &= \exists e. walking(e) \wedge walker(e, Sam) \wedge walkee(e, Spot) \end{aligned}\]
To compute the MR for ``Sam walks’’ we have: \[\begin{aligned} (\lambda P. P(Sam))[\lambda x. \exists e. walking(e) \wedge walker(e, x)]\\ &= (\lambda x. \exists e. walking(e) \wedge walker(e, x))[Sam]\\ &= \exists e. walking(e) \wedge walker(e, Sam) \end{aligned}\]
So, according to the meaning representations, “Sam walks” is entailed by “Sam walks Spot”: in every case where the latter is true, the former will also be true. However, in common usage, this entailment does not hold. For example, I might walk a dog by standing with a leash and letting the dog run around, or by riding a bicycle with the dog on a leash. This is different from the pair “Sam sees Spot”/“Sam sees” because in this case, the second sentence really is entailed by the first one.
The issue with “walk” is that the transitive form actually has a slightly different meaning from the intransitive form. It means something like “make someone/something walk”: the object of “walk” is the walker, not the subject. So we might consider changing the MR to something like the following, where \(y\) (which will be the object of the sentence) is now the walker instead of the walkee.