(No discussion questions here – due to midterm on Week 6. See instructions on Learn)
This week’s tutorial exercises focus on syntax, (English) grammar, and parsing, using context-free grammars. After working through the exercises you should be able to:
Provide examples showing how syntactic structure reflects the semantics of a sentence, and in particular, semantic ambiguity. You should also be able to explain and illustrate how constituency parses and dependency parses differ with respect to this issue.
Provide the syntactic parse for simple sentences using either Universal Dependencies or context-free grammar rules.
Hand-simulate the CKY parsing algorithm, and by doing so, better understand some of the computational issues involved.
When constructing a grammar and parsing with it, one important goal is to accurately reflect the meaning of sentences in the structure of the trees the grammar assigns to them. Assuming a compositional semantics, this means we would expect attachment ambiguity in the grammar to reflect alternative interpretations. The following two exercises aim to hone your intuitions about the syntax-semantics relationship.
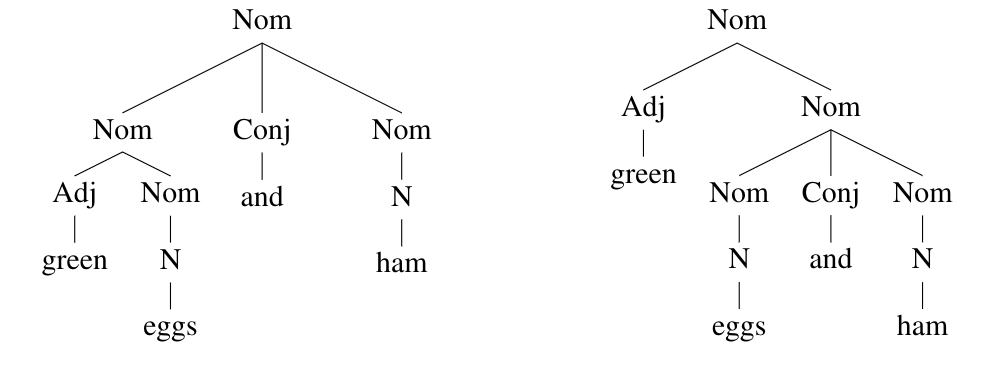
In English, conjunctions often create attachment ambiguity, as in the sentence I like green eggs and ham. The ambiguity inside the noun phrase here could be captured by the following two context-free grammar rules, where Nom is a nominal (noun-like) category:
Nom\(\;\rightarrow\;\)Adj Nom
Nom\(\;\rightarrow\;\)Nom Conj Nom
Write down two paraphrases of I like green eggs and ham, where each paraphrase unambiguously expresses one of the meanings.
Draw two parse trees for just the Nom part of the sentence, illustrating the ambiguity. You’ll also need to use a rule Nom\(\;\rightarrow\;\)N. Which tree goes with which paraphrase?
I like ham and green eggs or I like green eggs and green ham.
Respectively:

Another common source of attachment ambiguity in English is from prepositional phrases. The relevant grammar rules include:
VP\(\;\rightarrow\;\)V NP
VP\(\;\rightarrow\;\)VP PP
NP\(\;\rightarrow\;\)NP PP
PP\(\;\rightarrow\;\)P NP
Here are five verb phrases:
watched the comet from the roof with my telescope
watched the comet from the park across the street
watched a video by the BBC about the comet
watched a video about the expedition to the comet
watched a video about the comet on my mobile
Picture below shows five partial trees. Match the phrases to the trees which best capture their meanings. You may find it helpful to ask yourself questions such as “where did this event happen?",”how was it done?", "what was watched?". You may also want to try out (in pencil!) different ways of writing in phrases under the leaves of the various trees.
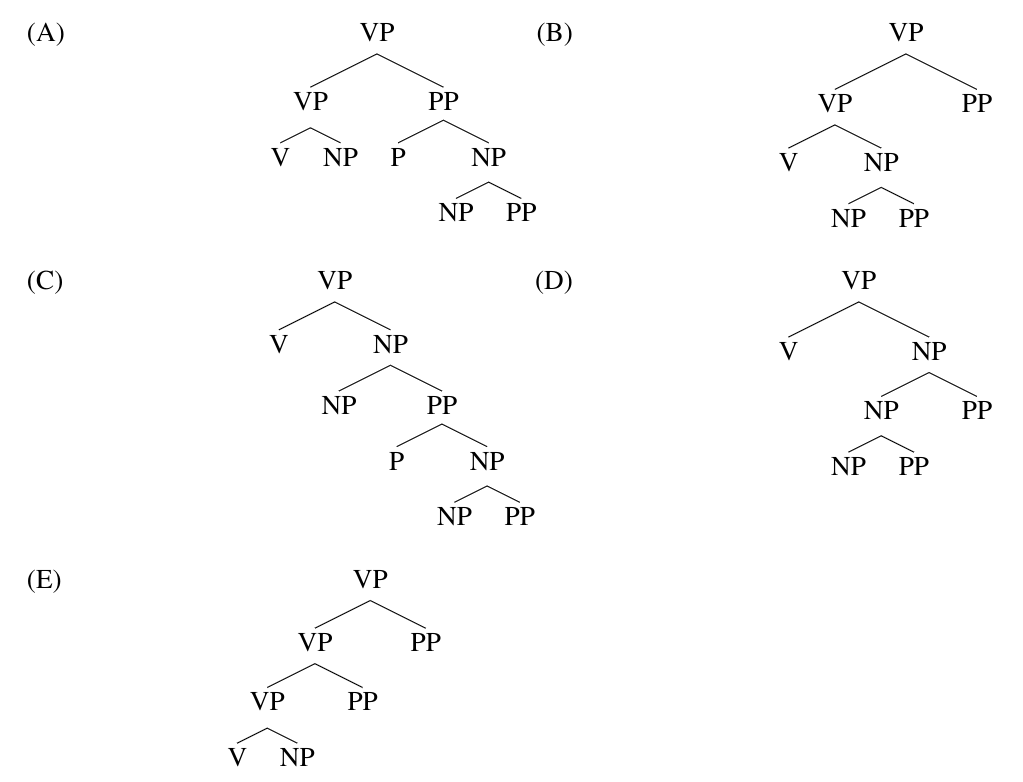
1E; 2A; 3D; 4C; 5B
Assume we are using the following grammar:
S\(\;\rightarrow\;\)NP VP \(\qquad\) V\(\;\rightarrow\;\)swam | ran | flew
VP\(\;\rightarrow\;\)V NP \(\qquad\) VP\(\;\rightarrow\;\)swam | ran | flew
VP\(\;\rightarrow\;\)VP PP \(\qquad\) D\(\;\rightarrow\;\)the | a | an
NP\(\;\rightarrow\;\)D N \(\quad \quad \quad\) N\(\;\rightarrow\;\)pilot | plane
NP\(\;\rightarrow\;\)NP PP \(\qquad\) NP\(\;\rightarrow\;\)Edinburgh | Glasgow
PP\(\;\rightarrow\;\)P NP \(\qquad\) P\(\;\rightarrow\;\)to
Draw a 7x7 chart for the sentence the pilot flew the plane to Glasgow and fill it in using the CKY algorithm. Number the symbols you put in the matrix in the order they would be computed, assuming the grammar is searched top-to-bottom.
How is the attachment ambiguity present in this sentence reflected in the chart at the end?
Here is a picture of the chart. To avoid clutter I included the backpointers only for the final three items added (the VPs and S). The backpointers show the (i,j) indices for the pair of child cells.
1 2 3 4 5 6 7
the pilot flew the plane to Glasgow
-----+-------+---------+-----+-------+----+-------
| | | | | |
0 1:D |9:NP |12:S | |15:S | |18:S [NP(0,2),VP(2,7)]
-----+-------+---------+-----+-------+----+-------
1 |2:N | | | | |
-----+-------+---------+-----+-------+----+-------
| | | | | |17:VP [VP(2,5),PP(5,7)]
2 | |3:V 4:VP | |13:VP | |16:VP [V(2,3),NP(3,7)]
-----+-------+---------+-----+-------+----+-------
3 | | |5:D |10:NP | |14:NP
-----+-------+---------+-----+-------+----+-------
4 | | | |6:N | |
-----+-------+---------+-----+-------+----+-------
5 | | | | |7:P |11:PP
-----+-------+---------+-----+-------+----+-------
6 | | | | | |8:NP
-----+-------+---------+-----+-------+----+-------The ambiguity isn’t represented explicitly at the top node. However if we follow the backpointer, we see that there are two VPs in (2,7), which indicates two distinct subtrees (with different backpointers).
It’s actually important that we do not add a second S at the top: if we carried the ambiguity upward in this fashion, we could end up storing an exponential number of categories in each cell—and this is exactly what we are trying to avoid.
Notice that the backpointers contain both the label and location of each child. For this example, the location alone would be enough because (for example) there is only one way to build a VP from the items in (2,5) and (5,7). But in principle there might be more than one rule that can make a VP from items in those cells, and in order to be able to efficiently reconstruct all of them at the end, we need to know the child’s label as well as its location. What we end up with at the end of parsing is called a “packed parse forest.”